Movimiento rectilíneo uniforme

El movimiento rectilíneo uniforme (también conocido por sus siglas como MRU) es aquel en el que se cumplen las siguientes dos condiciones: Los cuerpos se mueven en línea recta y la velocidad no varía respecto del tiempo.

Una característica del MRU, derivada de las condiciones anteriores, es que los móviles recorren distancias iguales en tiempos iguales. Además la aceleración es nula en todo el recorrido.

Velocidad en movimiento rectilíneo uniforme

La velocidad es una magnitud vectorial que mide con qué rapidez varía la posición de un móvil en el tiempo. En MRU es constante y su signo depende del sentido hacia dónde se mueva el móvil respecto a cómo definimos el sistema de referencia.

En el siguiente diagrama los móviles 1 y 2 tienen velocidad positiva (se dirigen en sentido positivo, independientemente de su posición) mientras que la velocidad de 3 es de signo negativo.



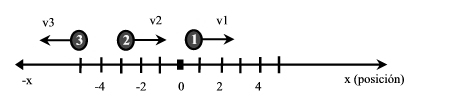
La velocidad la calculamos como la variación de la posición sobre la variación del tiempo. Para calcular el módulo de la velocidad podemos utilizar la siguiente expresión:


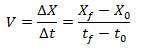
V = Velocidad [m/s]
ΔX = Variación de posición [m]
Δt = Variación de tiempo [s]
XF = Posición final [m]
X0 = Posición inicial [m]
tF = Tiempo final [s]
t0 = Tiempo inicial [s]

Como generalmente contamos el tiempo desde cero (es decir cuánto se tarda desde que empezamos a medir) muchas veces escribimos a la velocidad como:


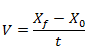
V = Velocidad [m/s]
XF = Posición final [m]
X0 = Posición inicial [m]
t = Tiempo en realizar el recorrido [s]

O bien si no utilizamos una referencia y sabemos cuánto espacio se recorrió y en que tiempo se hizo, calculamos la velocidad como:


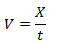
V = Velocidad [m/s]
X = Distancia recorrida [m]
t = Tiempo en realizar el recorrido [s]

El módulo de la velocidad se mide en unidades de espacio sobre unidades de tiempo, por ejemplo [m/s], [km/h]. Para la resolución de ejercicios de manera simple, es recomendable pasar todo a [m/s] y utilizar notación exponencial si fuesen números muy grandes o muy chicos.

Ejemplos

1) Si un móvil se encuentra en la posición X = 30 metros en el momento en que empezamos a contar el tiempo y 10 segundos después se encuentra en la posición X = 60 metros, entonces sabemos que su velocidad es de 3 [m/s] y su gráfico es: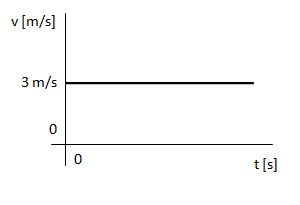


2) Si un móvil se encuentra en la posición X = 30 metros en el instante 0 y 5 segundos después se encuentra en la posición X = 10 metros (es decir se acercó al origen) su velocidad es de -4 [m/s] (*) y su gráfico es:



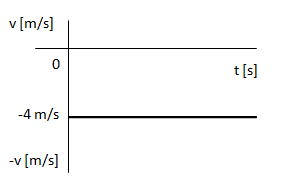
(*) En realidad podríamos decir que la velocidad siempre es positiva dado que avanza una cierta distancia por cada unidad de tiempo, pero dado un determinado sistema de referencia, si el móvil se desplaza para el lado negativo decimos que tiene velocidad negativa.

Debido a que estos gráficos son de la velocidad, no tomamos en cuenta la posición del móvil. El gráfico de la velocidad es independiente del lugar en dónde se encuentre. No importa si está del lado positivo o negativo, si sale o no desde origen, etc. Lo que sí nos importa es hacia dónde se mueve debido a que determina el signo de la velocidad.

Aceleración en movimiento rectilíneo uniforme

La aceleración mide la variación de la velocidad respecto del tiempo. En MRU es cero ya que la velocidad es constante, es decir que la velocidad inicial es igual a la velocidad final (no hay aceleración).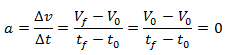

Gráfico de la aceleración

Gráfico de la aceleración respecto del tiempo en movimiento rectilíneo uniforme: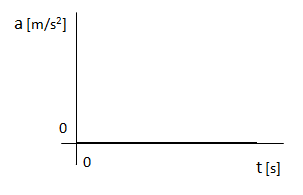

Posición respecto del tiempo en MRU

La fórmula con la que se calcula el lugar en dónde se encuentra un móvil suele llamarse ecuación horaria. Determina la posición en función de su velocidad (que es constante), del tiempo y de su posición inicial.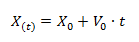


X(t): Posición que obtenemos como resultado en función del tiempo [m].
X0 = Posición inicial (dónde se encuentra el móvil en tiempo 0) [m].
V0 = Velocidad inicial. En MRU deberíamos llamarla V ya que es constante, pero para hacer las ecuaciones de MRU y MRUV lo más parecidas posibles utilizamos V0 (velocidad inicial) que también es correcto ya que la velocidad inicial es la misma en todo el recorrido [m/s].
t: Tiempo [s]

Si el origen de coordenadas coincide con el lugar desde donde parte el móvil entonces la posición inicial es 0, por lo tanto la distancia recorrida se calcula como la velocidad multiplicada por el tiempo.

Gráficos de ejemplo

1) Ejemplo de posiciones respecto del tiempo para dos velocidades distintas. Para cada velocidad, a igual tiempo recorre el mismo espacio.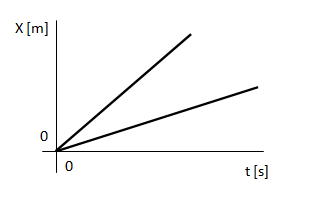



2) Móvil con velocidad negativa antes de tiempo cero, que pasa por el origen en t = 0 y continúa moviéndose con la misma velocidad negativa. Lo que decimos con velocidad negativa es que el móvil se dirige en sentido contrario hacia como planteamos el sistema.


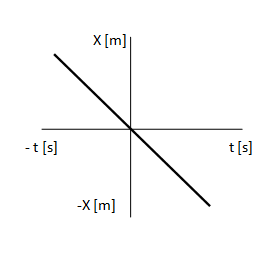
En los gráficos de posición respecto del tiempo en MRU, siempre obtenemos rectas (de mayor o menor pendiente de acuerdo a la velocidad, incluso de pendiente cero si está detenido).

Encuentro en movimiento rectilíneo uniforme

Los ejercicios de encuentro se utilizan para determinar en qué momento o en qué posición se encontrarán dos móviles. Los móviles se encuentran en el lugar donde su posición dentro del sistema de coordenadas sea la misma (donde tengan la misma X) para un mismo instante de tiempo. Por lo tanto para resolverlos planteamos dos ecuaciones horarias distintas (una para cada móvil) y las igualamos.

En el gráfico de posición respecto del tiempo tenemos líneas que se cruzan en la posición de encuentro. Sobre el eje X tenemos el tiempo de encuentro y sobre el eje Y la posición respecto del origen.

Gráficos de Ejemplo

1) En el siguiente ejemplo un móvil sale con velocidad inicial constante y positiva desde el origen y en el mismo momento otro móvil sale desde una determinada X positiva hacia el origen (es decir con velocidad de signo negativo).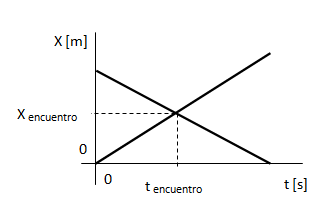

Ejercicios de velocidad en MRU

Ejercicio 1

Un cuerpo moviéndose con MRU pasa por un punto (A) a las 12:00:00 horas. Luego pasa por otro punto (B) ubicado a 30 km del primero a las 12:30:55 horas.

1. ¿Cuál es su velocidad?
2. Graficar la variación de la posición respecto del tiempo.

Solución

Por definición, la velocidad es la variación de la posición respecto del tiempo. Vamos a ubicar al sistema de referencia en el punto A y por lo tanto la posición inicial (X0) es 0 metros.

La posición final (XF) va a ser 30 km, que pasado a metros da 30000 metros. Entonces nos queda:


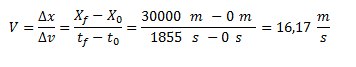
El gráfico lo realizamos de la siguiente manera:

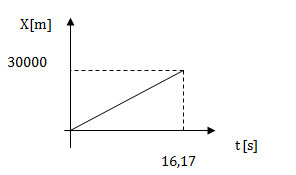
Ejercicio 2

Rehacer el ejercicio 1, ubicando el origen de coordenadas en el punto B y también considerando el sentido positivo hacia la derecha.

Solución

La posición inicial (X0) es -30000 metros, ya que la ubicamos a la izquierda del 0.

La posición final (XF) va a ser 0 metros, que es lo que se pide en el enunciado.

Entonces nos queda:


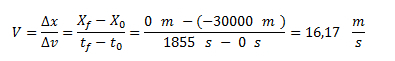
Observar que la velocidad vuelve a ser positiva debido a que en el nuevo sistema de referencia elegido el móvil se sigue moviendo en el mismo sentido que antes, es decir moviéndose hacia la derecha.

Ejercicio 3

- Convertir 35 km/h en m/s
- Convertir 1520 m/s en km/h

Solución

Para resolver este ejercicio utilizamos el método del factor de conversión, aunque podríamos realizar la conversión por cualquier método.

Ejercicio 4

Un móvil “A” viaja a 25 km/h y otro móvil “B” viaja a 5 m/s. ¿Cuál de los dos se mueve más rápido?

Solución

Para poder comparar las velocidades, tenemos que expresarlas con la misma unidad.

Para eso, convertimos una de las dos en la unidad de la otra, por ejemplo la del móvil “A” la pasamos a m/s.


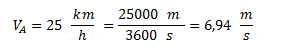
Como 6,94 m/s es mayor que 5 m/s, entonces el móvil “A” es el que viaja más rápido.


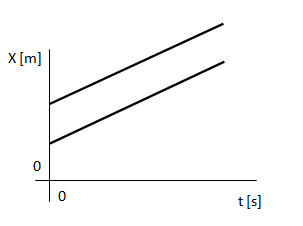
2) En el siguiente ejemplo dos móviles salen con velocidad positiva y del mismo módulo, desde distintas posiciones. No se encuentran.



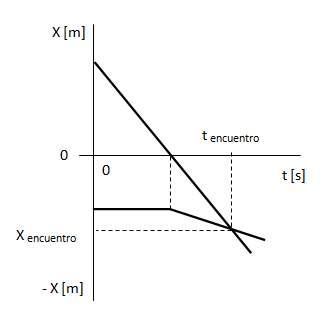
3) En el siguiente ejemplo un móvil sale con velocidad de signo negativo (yendo hacia el cero). Al pasar por el origen otro móvil que se encontraba detenido en una posición negativa empieza a avanzar también en el mismo sentido que el primero, pero a menor velocidad (notar la menor pendiente). Se encuentran en el tiempo te y en la posición Xe (que es negativa).

Ejercicios de posición en MRU

Ejercicio 1

Un móvil tiene una velocidad constante de 50 km/h. ¿Qué distancia recorrerá en 8 minutos y 40 segundos?

Solución

Aunque en este caso no sea necesario, vamos a pasar todo a las unidades básicas como venimos haciendo.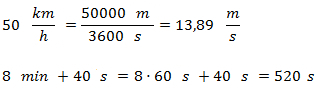




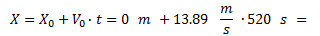
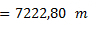
La distancia recorrida es 7,22 km.

Ejercicios de encuentro en MRU

Ejercicio 1

Un móvil parte a 10 km/h a las 12:00:00 en dirección este-oeste por una ruta rectilínea. A la misma hora, otro móvil que se encuentra a 80 km más adelante que el primero parte en sentido contrario (o sea en dirección al primero) con una velocidad de 25,5 km/h.

¿A qué hora se encuentran?

Solución

La ecuación horaria para el primer móvil es: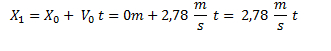


La ecuación horaria para el segundo móvil es:


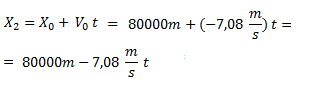
Igualamos las dos ecuaciones horarias y despejamos el tiempo:


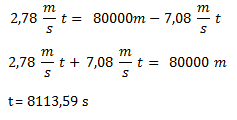
Se encuentran 2 horas, 15 minutos y 13 segundos después de la salida, es decir a las 14:15:13 horas.

Movimiento rectilíneo uniformemente variado

El movimiento rectilíneo uniformemente variado es aquel en dónde los cuerpos se mueven en línea recta y la velocidad a lo largo del recorrido varía respecto del tiempo. La velocidad puede aumentar (y en ese caso el movimiento es acelerado) o disminuir (y en ese caso es desacelerado).

Una característica de este movimiento es que, al variar la velocidad, el móvil recorre en tiempos iguales distancias distintas. La aceleración, que es la variación de velocidad respecto del tiempo, tiene un valor distinto de cero (positivo o negativo) y la distancia recorrida varía con el cuadrado del tiempo.

Aceleración en MRUV

El MRUV es un movimiento en el cual los móviles se desplazan en línea recta a una velocidadque varía de manera uniforme a lo largo del tiempo. Esta velocidad puede aumentar o disminuir.

La tasa de variación de la velocidad se denomina aceleración. Su valor puede ser positivo o negativo. La aceleración es una magnitud vectorial con lo cual, además de un módulo, tiene una dirección y un sentido.

Un signo negativo en la aceleración no necesariamente significa que la velocidad esté disminuyendo en valor absoluto. Puede estar aumentando en el sentido contrario al positivo del sistema de referencia fijado.

Si la velocidad viene disminuyendo y se hace cero sin que cambie la aceleración, el móvil se detendrá y comenzará a moverse en sentido contrario, esta vez aumentando su velocidad en valor absoluto. El vector que sí cambia de signo es el de la velocidad cuando comienza a moverse para el otro lado, pero la aceleración en este caso será la misma.

Signo de la aceleración

Si el móvil tiene velocidad de signo positivo y aumentando, la aceleración es positiva.

Si el móvil tiene velocidad de signo positivo y disminuyendo, la aceleración es negativa. Es decir que disminuye la velocidad hasta que se haga cero. Luego, con esta misma aceleración negativa, el móvil comenzará aumentar de velocidad (en módulo) pero con signo negativo.

Si el móvil tiene velocidad negativa y aumentando, la aceleración es negativa. La velocidad aumenta pero con en el signo contrario al sistema. Si el móvil se estaba moviendo antes de comenzar a contar el tiempo, en algún momento la velocidad podría haber sido cero (antes de ser negativa) y antes de eso positiva en disminución.

Si el móvil tiene velocidad negativa y disminuyendo, la aceleración es positiva. El móvil en algún momento se detendrá y comenzará a aumentar la velocidad en el sentido positivo (primer caso).

Valor de la aceleración

El valor de la aceleración se calcula como la variación de la velocidad en un tiempo determinado.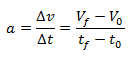


a = Aceleración [m/s2]
Δv = Variación de velocidad [m/s]
Δt = Variación de tiempo [s]
Vf = Velocidad final [m/s]
V0 = Velocidad inicial [m/s]
tF = Tiempo final [s]
t0 = Tiempo inicial [s]

Unidad de aceleración

La aceleración se mide en metros sobre segundos al cuadrado (m/s2).

Gráficos de ejemplo

Gráfico de la aceleración respecto del tiempo en el movimiento rectilíneo uniformemente variado.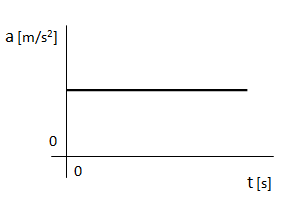

Velocidad en MRUV

La velocidad en función del tiempo se calcula desde la formula de aceleración: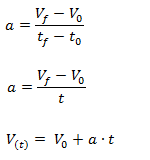



a = Aceleración [m/s2]
Vf = Velocidad final [m/s]
V0 = Velocidad inicial [m/s]
tf = Tiempo final [s]
t0 = Tiempo inicial [s]
t = Período de tiempo [s]
V(t) = Velocidad [m/s]

Es decir se multiplica la aceleración (cuánto varía la velocidad por cada unidad de tiempo) por el tiempo durante el cual está variando y se le suma la velocidad que tenía inicialmente.

Gráficos de ejemplo

1) Sin velocidad inicial, con velocidad en aumento.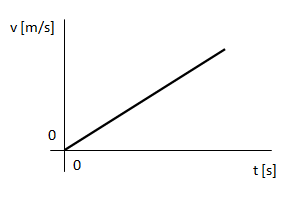



2) Con velocidad inicial, con velocidad en aumento.



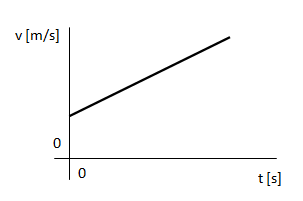
3) Con velocidad inicial, con velocidad en descenso.



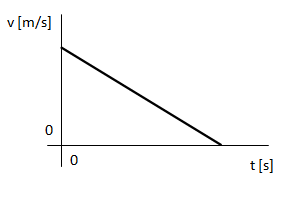
4) Con velocidad inicial, con velocidad en descenso. Al detenerse, comenzando a aumentar su velocidad en sentido contrario.

• Apéndice

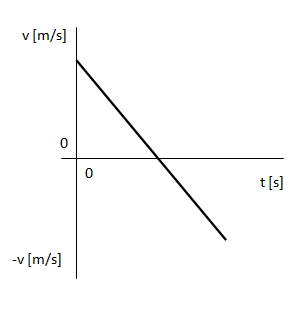
Posición respecto del tiempo en MRUV

La ecuación horaria de MRUV es: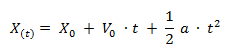


X(t) = Posición respecto del tiempo [m]
X0 = Posición inicial [m]
V0 = Velocidad inicial [m/s]
t = Tiempo [s]
a = Aceleración [m/s2]

Esta ecuación también sirve para movimiento rectilíneo uniforme, ya que en ese caso la aceleración es cero y reemplazando "a" por 0 queda la misma ecuación que conocemos del MRU.

Los siguientes gráficos de posición respecto del tiempo corresponden en el primer caso a un móvil que aumenta el módulo de su velocidad y en el segundo caso que lo disminuye.

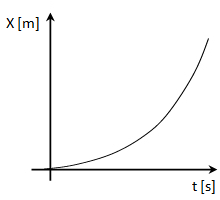
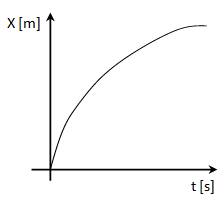
Relación entre la posición y el espacio recorrido

Existe una ecuación (derivada de las demás) que relaciona las velocidades inicial y final con el espacio recorrido y la aceleración (sin tener que conocer el tiempo).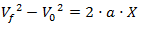


Vf = Velocidad final [m/s]
V0 = Velocidad inicial [m/s]
a = Aceleración [m/s2]
X = Distancia recorrida [m]

Encuentro en MRUV

El encuentro en MRUV se resuelve de manera similar a como se resuelve en MRU, es decir igualando las ecuaciones horarias. Incluso podemos plantear encuentro entre un móvil con MRU y otro con MRUV utilizando la respectiva ecuación horaria de cada uno.

Dado que hay valores elevados al cuadrado es posible tener en algunos casos tener dos tiempos de encuentro distintos e incluso uno positivo y otro negativo.

Ejemplos de dos tiempos de encuentro

Se podría dar el caso de que en un punto, un móvil que se mueve a velocidad constante pase a otro que se mueve en el mismo sentido a menor velocidad pero acelerando (que recién comience a moverse). Luego el segundo móvil aumentará su velocidad y lo volverá a pasar al primero, es decir hay 2 encuentros.

Otro caso podría ser el de dos móviles moviéndose en sentido contrario y desacelerando. Se cruzan una vez, luego siguen disminuyendo la velocidad hasta que se hace cero y luego comienzan a moverse en sentido contrario debido a que mantienen su misma aceleración. También se encuentran dos veces.

Salidas a diferente horario

Cuando dos o más móviles parten a diferente horario, lo más conveniente es calcular primero la posición de cada uno de ellos para un mismo instante (por ejemplo t=0) y una vez hecho esto volver a plantear las ecuaciones horarias. Esto evita tener sumas y restas elevadas al cuadrado en el término “t”.

Tiro vertical y caída libre

Estos movimientos se resuelven con las mismas ecuaciones de MRUV, tomando como aceleración la de la gravedad de la tierra, que en vez de "a" la llamamos "g". La aceleración de la tierra también es una magnitud vectorial y su módulo es: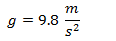


Su signo depende de cómo ubiquemos el sistema de referencia. Si el sistema lo ponemos creciente desde la tierra hacia arriba entonces g tiene signo negativo.

Debido a que trabajamos con sistemas coordenados, utilizamos la misma fórmula para el tiro vertical que para la caída libre (que además son las mismas formulas que utilizamos para todo MRUV). Tomamos positiva a la aceleración cuando hace aumentar a la velocidad en el sentido que crece el sistema de referencia y negativa en el otro caso.

Tiro Vertical

El tiro vertical corresponde al movimiento en el cual se lanza un objeto en línea recta hacia arriba con una velocidad inicial.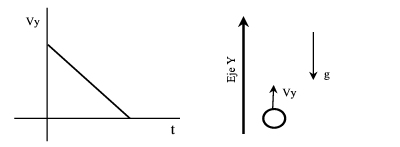

Caída Libre

La caída libre corresponde al movimiento en dónde se deja caer un objeto. El siguiente gráfico corresponde a la velocidad durante la caída libre, poniendo un sistema de coordenadas con el origen en el piso y dirigido hacia arriba, es decir la velocidad tiene signo negativo.

Con esta disposición, la aceleración también tiene signo negativo. En el gráfico consideramos velocidad inicial nula. Si realizamos un ejercicio completo de tiro vertical y caída libre, hay que tener en cuenta que en el tiro vertical sí tenemos velocidad inicial, pero la caída libre es otro movimiento que comienza justamente cuando esa velocidad es cero.

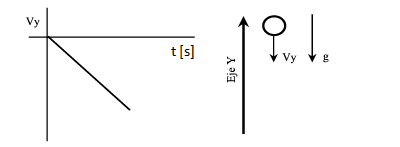
Características del tiro vertical y la caída libre

En ambos casos se toman en cuenta las velocidades iniciales y las distancias, pero no intervienen el peso o la masa para calcular la altura o el tiempo.

Debería importar la forma de los objetos con el fin de calcular el rozamiento con el aire (que ejerce una fuerza), pero no lo consideramos en estos ejercicios.

Para el tiro vertical, en el caso de que utilicemos un sistema de referencia dirigido hacia arriba, la aceleración tiene signo negativo y velocidad inicial positiva. En la caída libre, con el mismo sistema de referencia, la velocidad es negativa (en aumento) y la aceleración no cambia de signo (con ese sistema seguiría siendo negativa).

Tiro oblicuo

Muchas veces la trayectoria de un móvil no es en línea recta. En esta sección vamos a analizar especialmente aquellos casos en donde actúa la aceleración de la gravedad.

Para resolver este tipo de ejercicios se suele descomponer el movimiento y la velocidad en los ejes "X" e "Y" y calcular los movimientos por separado. En los ejemplos siguientes, sobre el eje vertical (Y) tenemos un MRUV con la aceleración de la gravedad y sobre el horizontal un MRUcon la velocidad calculada VX.

Por lo tanto para resolver ejercicios de tiro oblicuo primero descomponemos la velocidad inicial en X e Y (con las funciones coseno y seno).

Ejemplos

Lanzamiento de una bala de cañón. Lo primero que hacemos en este caso es descomponer las velocidades.

Si debido al ángulo aparece una componente VY (sobre el eje Y) habrá primero un movimiento similar a un tiro vertical (con velocidad inicial VY) y luego una caída libre (con velocidad inicial 0).Todo esto mientras en X hay un MRU (con velocidad VX).



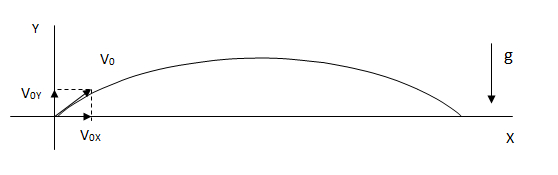
En este caso la velocidad en X es constante:



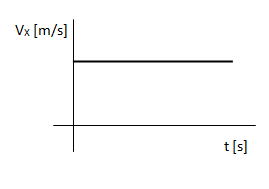
La velocidad en Y varía con la aceleración de la gravedad. En este ejemplo primero va disminuyendo hasta hacerse cero (como un tiro vertical) y luego comienza a aumentar en sentido contrario (como una caída libre).



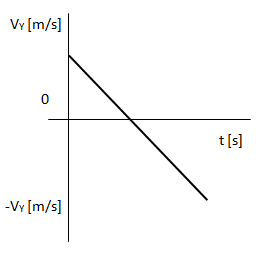
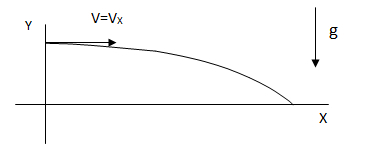
Si por ejemplo se tratase de un tiro horizontal (paralelo a X) no hay VY y por lo tanto sobre el eje Y tenemos únicamente una caída libre desde la altura del tiro hasta el piso.



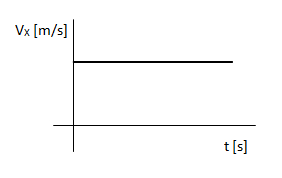
Al igual que en el caso anterior, la velocidad en X es constante.



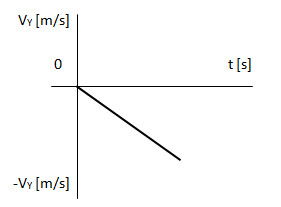
El gráfico de la velocidad en Y es similar al de una caída libre.

Ejercicios de aceleración en MRUV

Ejercicio 1

Un móvil se mueve con una velocidad constante de 15 km/h. A partir de un determinado momento t=0 comienza a acelerar y 15 segundos después su velocidad es de 50 km/h.

¿Cuál es su aceleración a partir de t=0?

Solución

Primero convertimos ambas velocidades a metros sobre segundo.


Lugo planteamos la fórmula de la definición de aceleración.

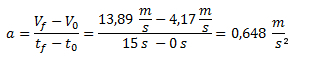
Ejercicio 2

Un móvil viaja a 40 km/h y comienza a reducir su velocidad a partir del instante t=0. Al cabo de 6 segundos se detiene completamente.

¿Cuál fue aceleración durante el período en el que redujo su velocidad?

Solución

Primero convertimos la velocidad inicial a m/s.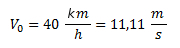


Luego planteamos la ecuación de la aceleración:

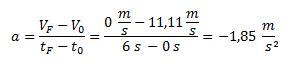
Ejercicio 3

Un tren viaja a 60 km/h. Inmediatamente después de pasar una señal en rojo comienza a detenerse. Se detiene completamente a los 150 metros.

Determinar su aceleración.

Solución

Ubicamos el sistema de referencia en el mismo lugar en el que se encuentra la señal y pasamos la velocidad a m/s.

V0 = 60 km/h = 16,67 m/s

Despejamos la aceleración de la ecuación que relaciona la posición con el espacio recorrido.


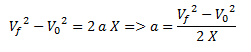
Reemplazamos por los valores y calculamos la aceleración


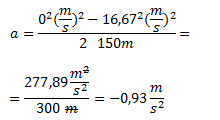
Notar que la aceleración tiene signo negativo ya que el tren está disminuyendo la velocidad moviéndose hacia el lado positivo del sistema de referencia.

Ejercicios de velocidad en MRUV

Ejercicio 1

Un móvil viaja a 60 kilómetros por hora. A partir de t=0 comienza a acelerar a razón de 4 m/s2.

¿Cuál es su velocidad al cabo de 0,1 minuto?

Solución

Convertimos 60 km/h a m/s.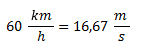


Planteamos la ecuación de la velocidad y reemplazamos por los valores del ejercicio.

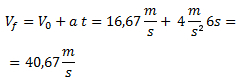
Ejercicio 2

Un móvil se desplaza con velocidad inicial desconocida. A partir de t=0 comienza a acelerar a 1,5m/s2. Luego de 10 segundos se desplaza a 100 km/h.

Determinar la velocidad inicial.

Solución

Convertimos 100 km/h a m/s.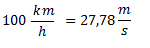


Despejamos la velocidad inicial de la ecuación de velocidad.


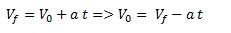
Reemplazamos por los datos del ejercicio y obtenemos el resultado.

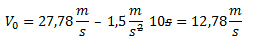
Ejercicios de posición en MRUV

Ejercicio 1

Un móvil con una velocidad inicial de 10 km/h comienza a acelerar en t=0 a razón de 6 m/s2.

¿Qué distancia recorre durante los 20 segundos siguientes a partir del instante en que comienza a acelerar?

Solución

Convertimos 10 km/h a m/s.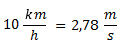


Definimos X0 (posición inicial) = 0 m, debido a que queremos conocer la distancia a partir de ese punto. Planteamos la ecuación horaria y resolvemos.

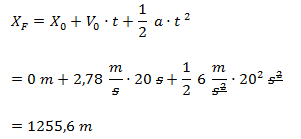
Ejercicio 2

Un tren viaja a una velocidad constante de 70 km/h y pasa una señal en rojo. A 60 metros de pasar la señal comienza a reducir su velocidad a razón de 2 m/s2.

¿A qué distancia de la señal se detiene por completo?

¿Cuánto tarda en hacerlo a partir del momento en el que pasa la señal?

Solución

Pasamos la velocidad inicial a m/s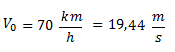


Ubicamos el sistema de referencia con el 0 en la señal, debido a que queremos conocer la posición respecto de ese punto.

El t=0 lo fijamos en el momento en que el tren comienza a disminuir la velocidad, debido a que es a partir de ese momento cuando el movimiento comienza a ser variado (MRUV).

La posición inicial (del MRUV) es de 60 m, ya que es la distancia desde la señal en t=0.


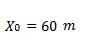
El signo de la aceleración es negativo, ya que apunta hacia el 0, en contra del sistema de referencia (el tren está disminuyendo la velocidad).


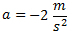
El tiempo que tarda en detenerse (a partir de que comienza a disminuir la velocidad) lo calculamos a partir de la fórmula de la aceleración.


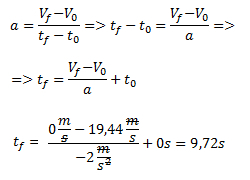
Ahora podemos plantear la ecuación horaria y responder la primera pregunta.


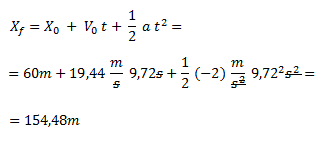
El tiempo que tarda en detenerse a partir del momento en que pasa la señal es el tiempo correspondiente a los primeros 60 metros (en los que viaja con MRU) sumado al tiempo que tarda en detenerse desde que comienza a disminuir la velocidad. Este último tiempo ya lo tenemos calculado, por lo que solo resta calcular el primero. Para eso lo despejamos de la ecuación de velocidad en MRU.


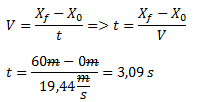
Por lo tanto el tiempo que tarda en detenerse (a partir de pasar la señal) es:

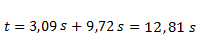
Ejercicios de encuentro en MRUV

Dos vehículos separados por 10 km parten al encuentro en el instante t=0. El primero lo hace con una velocidad inicial constante de 10 km/h. El segundo parte desde el reposo y con una aceleración de 0,5 m/s2.

¿A qué distancia de la salida del primer vehículo se encuentran?

Solución

Lo primero que hacemos es plantear un sistema de referencia. Ubicamos el 0 en la posición del primer vehículo. Indicamos también la velocidad del primer móvil en m/s.


Luego planteamos las ecuaciones horarias de cada móvil.

Ecuación del móvil A:


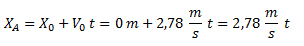
Planteamos la ecuación del móvil B. Este móvil no tiene velocidad inicial (ya que parte desde el reposo) y por lo tanto simplificamos ese término.


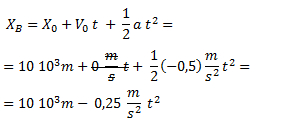
Igualamos ambas ecuaciones y despejamos el tiempo:


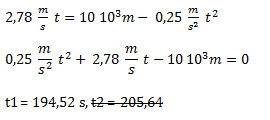
Se encuentran a los 194,52 segundos de la partida, es decir a los 3 minutos y 15 segundos.

Para conocer la posición, reemplazamos este tiempo en cualquiera de las ecuaciones horarias (ya que el sistema de referencia es el mismo y obtenemos la posición desde el punto de salida del primer móvil).

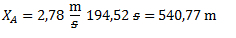
Ejercicios de tiro vertical y caída libre

Ejercicio 1

Se lanza verticalmente y hacia arriba un cuerpo con una velocidad inicial de 20 m/s.

¿Cuál es la altura máxima que alcanza?

¿En qué tiempo alcanza esa altura?

Solución

Lo primero que hacemos es plantear un sistema de referencia. Elegimos plantearlo en el mismo sentido que la velocidad inicial, por lo tanto la gravedad (que apunta en sentido contrario al sistema de referencia) tiene signo negativo.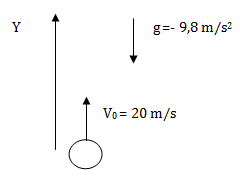

Planteamos la relación entre velocidad final, inicial, distancia y aceleración en MRUV y despejamos la distancia.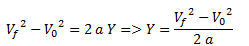


Sabemos que la altura máxima se alcanza cuando la velocidad final es 0. Reemplazamos los valores y obtenemos la distancia.


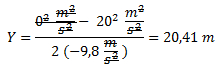
Para obtener el tiempo que tarda en alcanzar la altura máxima, lo despejamos de la ecuación horaria de MRUV.


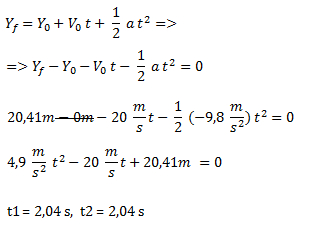
La altura máxima la alcanza en 2,04 s.