Trabajo
El trabajo es el producto escalar de la fuerza (vector) por el desplazamiento (vector). Al ser un producto escalar, el trabajo también es una magnitud escalar, siendo igual al producto de los módulos de ambos vectores por el coseno del ángulo que forman.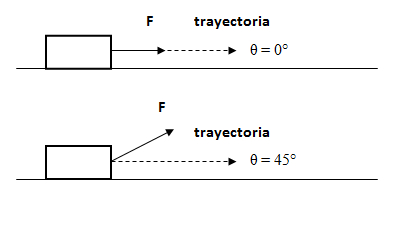
Si la fuerza es constante, calculamos el trabajo como:
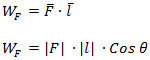
WF = Trabajo de la fuerza F [J]
F = Fuerza [N]
l = Desplazamiento [m]
θ = Ángulo [grados o radianes]
Cuando la fuerza no es constante el trabajo se calcula como la integral de la fuerza por el desplazamiento:
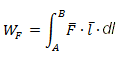
Unidad de trabajo
En el Sistema Internacional de Unidades, la unidad del trabajo es el joule y representa al trabajo realizado por una fuerza de un newton a lo largo de un metro:
Trabajo Nulo
Para que haya trabajo debe haber desplazamiento. Hay fuerzas que no realizan trabajo.Algunos ejemplos
En el desplazamiento de un cuerpo sobre una superficie, la normal no realiza trabajo ya que el coseno del ángulo entre los vectores fuerza y desplazamiento vale cero.La fuerza peso no realiza trabajo en un desplazamiento horizontal. Si en cambio el cuerpo sube y baja volviendo al mismo lugar hay un trabajo positivo y otro negativo, por lo que tampoco se realiza trabajo volviendo al mismo punto.
El trabajo vale cero si
- Desplazamiento = 0
- Cos θ = 0
- F = 0
Fuerzas conservativas y no conservativas
Dentro de las fuerzas que sí realizan trabajo encontramos dos grupos, las fuerzas conservativas y las no conservativas.Fuerzas conservativas
Las fuerzas conservativas son aquellas en las que el trabajo a lo largo de un camino cerrado es nulo. El trabajo depende de los puntos inicial y final y no de la trayectoria.Fuerzas no conservativas
En contraposición, las fuerzas no conservativas son aquellas en las que el trabajo a lo largo de un camino cerrado es distinto de cero. Estas fuerzas realizan más trabajo cuando el camino es más largo, por lo tanto el trabajo no es independiente del caminoPotencia
La potencia es la cantidad de trabajo realizado por unidad de tiempo. Se calcula como: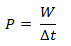
P = Potencia [W]
W = Trabajo [J]
Δt = Intervalo de tiempo [s]
Unidad de potencia
La unidad de potencia en el Sistema Internacional es el watt y equivale a: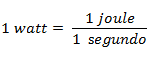
También se define la potencia eléctrica, analizada en la sección de electricidad.
Energía
La energía se define como la capacidad de producir trabajo, por lo tanto también se mide en joule. Un joule de energía puede producir un joule de trabajo. Existen distintos tipos de energía tales como la eléctrica, nuclear, química, mecánica, etc.Energía mecánica
La energía mecánica es la suma de la energía potencial y la energía cinética de un cuerpo. A su vez la energía potencial suele considerarse formada por la suma de la energía potencial gravitatoria y potencial elástica. Por lo tanto la energía mecánica la podemos definir como: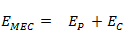
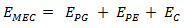
EMEC = Energía mecánica [J]
EP = Energía potencial [J]
EC = Energía cinética [J]
EPG = Energía potencial gravitatoria [J]
EPE = Energía potencial elástica [J]
Energía potencial
La energía potencial es aquella que tiene un cuerpo debido a su posición en un determinado momento. Por ejemplo un cuerpo que se encuentra a una cierta altura puede caer y provocar un trabajo o un resorte comprimido o estirado puede mover un cuerpo también produciendo trabajo.La energía potencial la consideramos como la suma de las energías potencial gravitatoria y potencial elástica, por lo tanto:
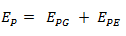
Energía potencial gravitatoria (EPG)
Es la que tienen los cuerpos debido a la gravedad de la tierra. Se calcula multiplicando el peso por la altura. Se suele considerar que a una altura cero la EPG es cero, por lo tanto se calcula como: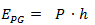
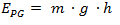
EPG = Energía potencial gravitatoria [J]
P = Peso del cuerpo [N]
h = Altura a la que se encuentra [m]
m = Masa del cuerpo [kg]
g = Aceleración de la gravedad [m/s2]
Energía potencial elástica (EPE)
Es la energía acumulada en un cuerpo elástico tal como un resorte. Se calcula como: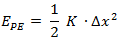
EPE = Energía potencial elástica [J]
K = Constante del resorte [N/m]
Δx = Desplazamiento desde la posición normal [m]
Energía cinética
Es la energía que tiene un cuerpo debido a su velocidad. Se calcula como: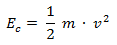
EC = Energía cinética [J]
m = Masa del cuerpo [kg]
v = Velocidad a la que se desplaza [m/s]
Impulso y cantidad de movimiento
Impulso
El impulso es el producto entre una fuerza y el tiempo durante el cual está aplicada. Es una magnitud vectorial. El módulo del impulso se representa como el área bajo la curva de la fuerza en el tiempo, por lo tanto si la fuerza es constante el impulso se calcula multiplicando la F por Δt, mientras que si no lo es se calcula integrando la fuerza entre los instantes de tiempo entre los que se quiera conocer el impulso.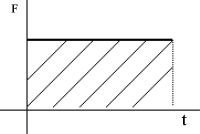
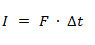
I = Impulso [kg·m/s]
F = Fuerza [N]
Δt = Intervalo de tiempo [s]
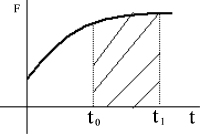
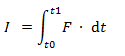
I = Impulso [kg·m/s]
F = Fuerza [N]
t0, t1 = Intervalo de tiempo [s]
Unidad de impulso
El impulso se mide en kg·m/s, una unidad equivalente a N·s.Cantidad de Movimiento
La cantidad de movimiento o momento lineal es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
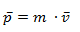
p = Cantidad de movimiento [kg·m/s]
m = Masa [kg]
v = Velocidad [m/s]
Unidad de cantidad de movimiento
La cantidad de movimiento se mide en kg·m/s. Tiene la misma unidad que el impulso aunque sean conceptos diferentes.Relación entre impulso y la cantidad de movimiento
El impulso aplicado a un cuerpo es igual a la variación de la cantidad de movimiento, por lo tanto el impulso también puede calcularse como: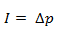
Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de la masa:
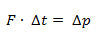
Características de los choques
Cuando dos cuerpos chocan sin que actúen fuerzas externas, se conserva la cantidad de movimiento total del sistema (para cualquier tipo de choque). Sin embargo pueden variar la cantidad de movimiento de cada uno de los cuerpos.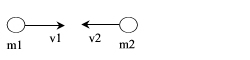
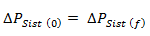
Δpsist(0) = Cantidad total de movimiento antes del choque
Δpsist(f) = Cantidad total de movimiento después del choque
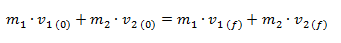
m1, m2 = Masa de los cuerpos 1 y 2 [kg]
v1(0), v2(0) = Velocidades iniciales de los cuerpos 1 y 2 [m/s]
v1(f), v2(f) = Velocidades finales de los cuerpos 1 y 2 [m/s]
Dependiendo de que ocurra con los cuerpos, luego del choque podemos encontrar distintos tipos de choque.
Coeficiente de restitución
Cuando dos cuerpos chocan, sus materiales pueden comportarse de distinta manera según las fuerzas de restitución que actúen sobre los mismos. Hay materiales cuyas fuerzas restituirán completamente la forma de los cuerpos sin haber cambio de forma ni energía cinética perdida en forma de calor, etc. En otros tipos de choque los materiales cambian su forma, liberan calor, etc., modificándose la energía cinética total.Se define entonces un coeficiente de restitución (K) que evalúa esta pérdida o no de energía cinética, según las fuerzas de restitución y la elasticidad de los materiales.
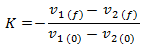
K = Coeficiente de restitución [sin unidad]
V1(0), V2(0) = Velocidades de los cuerpos 1 y 2 antes del choque
V1(f), V2(f) = Velocidades de los cuerpos 1 y 2 después del choque
K es un número que varía entre 0 y 1.
Si K = 0 choque perfectamente inelástico.
Si 0 < K < 1 choque semielástico.
Si K = 1 choque perfectamente elástico.
Tipos de choque
Choque elástico
En un choque elástico, además de la cantidad de movimiento, también se conserva la energía cinética total del sistema.También se conservan las formas de los cuerpos y no hay energía perdida por rozamiento, calor, etc. El coeficiente de restitución en este tipo de choque vale 1.
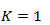
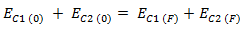
K = Coeficiente de restitución [sin unidad]
Ec1(0), Ec2(0) = Energía cinética inicial de los cuerpos 1 y 2 [J]
Ec1(f), Ec2(f) = Energía cinética final de los cuerpos 1 y 2 [J]
Choque inelástico o semielástico
En la mayoría de los casos reales actúan fuerzas que no restituyen completamente las formas, habiendo pérdidas de energía cinética. Esto es cuando K tiene valores mayores que 0 y menores que 1. En ese caso decimos que el choque es inelástico o semielástico.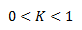
Choque perfectamente inelástico
El choque perfectamente inelástico se da cuando ambos cuerpos quedan pegados, teniendo una sola masa luego del choque. Al haber un cambio de forma no se conserva la energía cinética de los cuerpos. El coeficiente de restitución en este tipo de choque vale 0.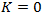
Ejercicios resueltos de choque
Ejercicio 1
Los siguientes cuerpos chocan de forma elástica.Calcular la velocidad final V2.
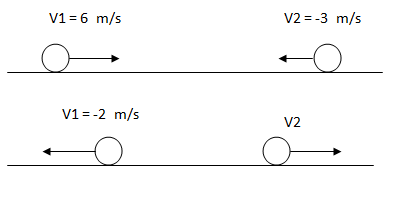
Solución
Como nos dicen que se trata de un choque elástico, sabemos que el coeficiente de restitución es igual a 1. Por lo tanto planteamos la fórmula del coeficiente de restitución y despejamos la velocidad del segundo cuerpo.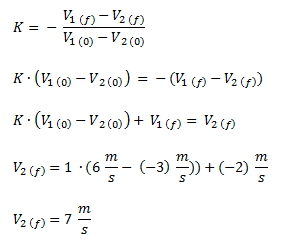
Ejercicio 2
Un cuerpo de 2 kg de masa se dirige en línea recta a 5 m/s hacia otro cuerpo de 3 kg que se encuentra detenido. Luego del choque ambos cuerpos quedan pegados.Calcular la velocidad final de los mismos.
Solución
Planteamos la fórmula de conservación de la cantidad de movimiento.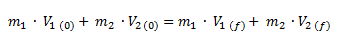
Como sabemos que ambos cuerpos quedan pegados, reemplazamos las dos velocidades finales por una sola (Vf).
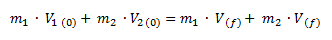
Despejamos la velocidad final del sistema y reemplazamos por los valores del ejercicio.
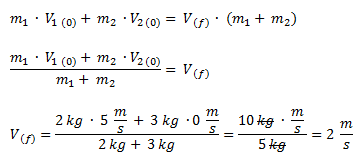
Ejercicio 3
Determinar la velocidad final de m2 y el tipo de choque.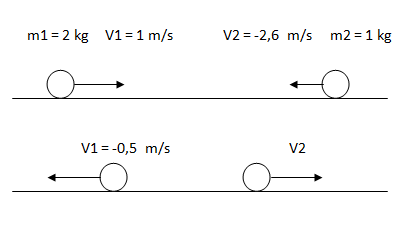
Solución
Planteamos la fórmula de conservación de la cantidad de movimiento y despejamos la velocidad final del segundo cuerpo.Para determinar el tipo de choque calculamos el coeficiente de restitución.
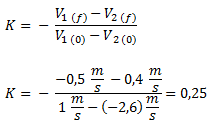
Como K es un valor mayor que cero y menor que uno, resulta un choque inelástico (o semielástico).
Ejercicios de trabajo
Ejercicio 1
Calcular el trabajo que realiza la fuerza F sobre la distancia d.Datos F = 15 N, θ = 35°, d = 2 m.
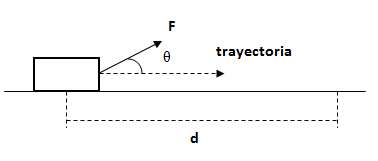
Solución
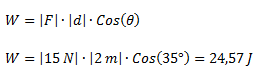
Ejercicio 2
Calcular el trabajo que realiza la fuerza F y la fuerza de rozamiento FR sobre la distancia d.Datos m = 10 kg, F = 100 N, θ = 35°, d = 10 m, μd = 0,1.
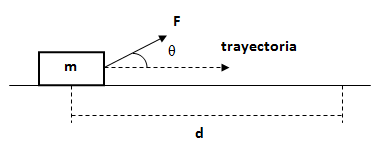
Solución
Calculamos el peso del bloque. Indicamos sólo su módulo: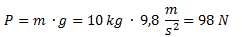
Calculamos el módulo de la fuerza normal, que en este caso es igual al peso ya que la superficie es horizontal y no hay otras fuerzas actuando.
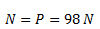
Calculamos el valor de la fuerza de rozamiento dinámico como el producto del coeficiente de rozamiento por la fuerza normal. También indicamos su módulo solamente.
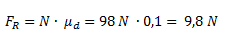
Finalmente calculamos el trabajo de las dos fuerzas.
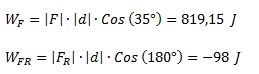
Ejercicio 4
Calcular el trabajo de la siguiente fuerza.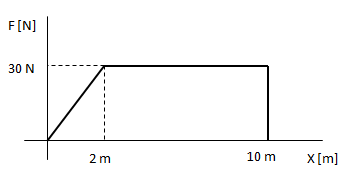
Solución
El trabajo total realizado lo podemos calcular como el área bajo la curva.Lo planteamos como la suma de dos trabajos parciales: el correspondiente al tramo en el que la fuerza es variable (área de un triángulo) y el correspondiente al tramo en el que la fuerza es constante (área de un rectángulo).
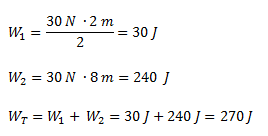
Ejercicio 5
Una grúa sube en forma vertical un bloque hasta una altura de 4 m, a velocidad constante y en un tiempo de 10 s. La potencia disipada para realizar ese trabajo es de 2000 W.¿Cuál es el peso del bloque?
Solución
Planteamos la fórmula de potencia y despejamos el trabajo realizado.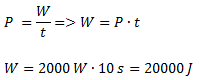
Planteamos la fórmula de trabajo y despejamos la fuerza, que es igual al peso.
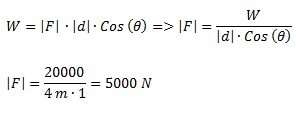
Ejercicio 6
Una bomba sube 1 m3 de agua a una altura de 30 m en 15 minutos.¿Cuál es el trabajo realizado por la bomba?
¿Cuál es la potencia empleada?
Datos: Peso específico del agua: 9800 N/m3.
Solución
Planteamos la fórmula de trabajo y reemplazamos por los valores del ejercicio: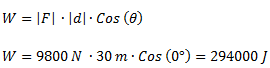
Para el cálculo de la potencia, convertimos los minutos a segundos, planteamos la fórmula de potencia y reemplazamos los valores.
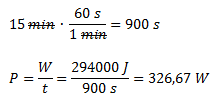
Ejercicio 7
Se sube un bloque de 20 kg por un plano inclinado de 30° y 5 metros de altura a través de una cuerda y a velocidad constante. El coeficiente de rozamiento dinámico entre el bloque y la superficie del plano es de 0,25.Hallar el trabajo realizado por las siguientes fuerzas: tensión de la cuerda, fuerza de rozamiento, peso, normal.
Solución
Hacemos un diagrama con la situación planteada en el ejercicio.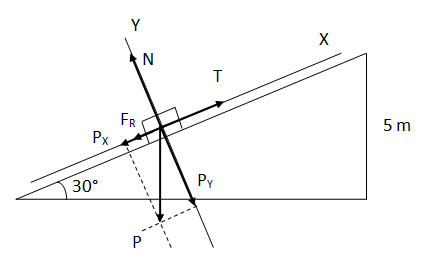
Calculamos el peso del bloque. Para simplificar las cuentas indicamos solo los módulos de las fuerzas y luego sumamos o restamos según el signo del esquema.
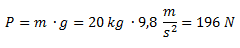
Calculamos las componentes del peso en los ejes X e Y.
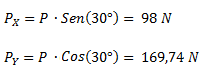
Planteamos la sumatoria de fuerzas en el eje Y. Despejamos la fuerza normal.
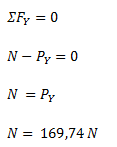
Calculamos la fuerza de rozamiento en base a la fuerza normal y al coeficiente de rozamiento.
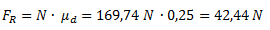
Planteamos la sumatoria de fuerzas en el eje X y despejamos la tensión de la cuerda.
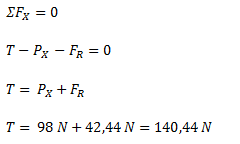
Calculamos la distancia sobre el plano (d) por medio de relaciones trigonométricas.
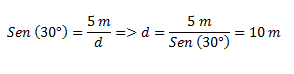
Finalmente calculamos el trabajo de cada fuerza, multiplicando los módulos de cada una de las fuerzas por la distancia recorrida y por el coseno del ángulo entre la fuerza y la trayectoria.
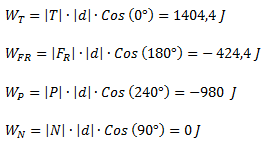
Ejercicio 8
Una presa tiene un caudal de 10 m3/min y una altura de 5 m.Calcular la potencia eléctrica generada, asumiendo una eficiencia del 100%.
Dato: Peso específico del agua = 9800 N/m3.
Solución
Pasamos el tiempo a unidades básica del Sistema Internacional.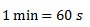
Planteamos la fórmula de potencia y reemplazamos al trabajo por el producto de la fuerza por la distancia.
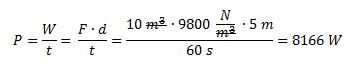
Ejercicios de energía
Ejercicio 1
Calcular la energía mecánica correspondiente al siguiente móvil.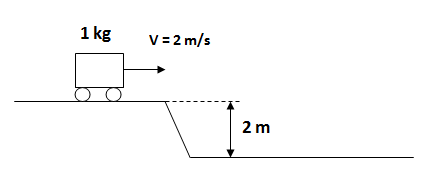
Solución
Planteamos a la energía mecánica como la suma de la energía cinética y la energía potencial gravitatoria.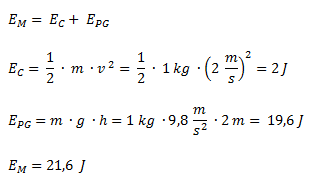
Ejercicio 2
Hallar la energía mecánica de un avión de 5000 kg que vuela a 2000 metros de altura a una velocidad de 350 km/h.Solución
Convertimos la velocidad a unidades básicas del Sistema Internacional utilizando el método del factor de conversión.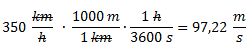
La energía mecánica la calculamos como la suma de la energía cinética y la energía potencial gravitatoria.
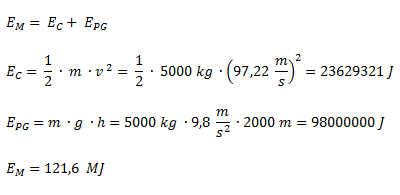
No hay comentarios.:
Publicar un comentario