MOVIMIENTO ARMÓNICO
El movimiento de un péndulo, las oscilaciones de la cuerda de un piano, o la membrana de unos altavoces. Son distintos ejemplos en los que el movimiento se produce alrededor de un punto de equilibrio.
En este tema estudiaremos el movimiento armónico simple, esencial para comprender el movimiento ondulatorio que estudiaremos en temas posteriores y en base al cual se producen fenómenos tan importantes como el sonido o la luz. Lo estudiaremos desde el punto de vista cinemático, dinámico y energético y veremos algunos ejemplos de cuerpos que se comportan siguiendo este tipo de movimiento.
Para abordar los contenidos de este tema, te recomendamos que estés familiarizado con los temas de cinemática, dinámica y energía vistos en niveles anteriores. Además, para comprendedlos en su totalidad, es ideal que tengas dominio de aritmética, trigonometría y álgebra básicas, vectores y derivadas e integrales a nivel básico
.Decimos que una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando vibra bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio. Decimos, entonces, que dicho cuerpo es un oscilador armónico. En este apartado estudiaremos:
- El concepto de vibración u oscilación y sus tipos
- La definición del m.a.s. y sus características principales
- Las magnitudes que lo definen
- Su gráfica de posición
- Algunos casos típicos de m.a.s. en tu día a día
Adicionalmente, es posible que tengas interés en profundizar en el comportamiento del m.a.s. Te aconsejamos que visites:
Vamos allá.
Oscilaciones y Vibraciones
¿Sabrías decir qué tienen en común un péndulo, el latido de tu corazón, la membrana de los altavoces de tu equipo de música o el mecanismo de un reloj? Se podría decir, en un sentido figurado, que todos ellos generanoscilaciones o vibraciones que nos marcan el ritmo. En este apartado vamos a explicar las características qué tienen en común todos estos movimientos y para ello vamos a presentar el movimiento armónico simple (m.a.s.) también conocido como movimiento vibratorio armónico simple (m.v.a.s.).
Para entender el movimiento armónico simple es importante entender el concepto de oscilación o vibración. Los cuerpos oscilan o vibran cuando se apartan de su posición de equilibrio estable.
Decimos que un cuerpo oscila o vibra cuando se mueve de forma periódica en torno a una posición de equilibrio debido al efecto de fuerzas restauradoras. Las mágnitudes características de un movimiento oscilatorio o vibratorio son:
- Periodo (T): El tiempo que tarda de cumplirse una oscilación completa. Su unidad de medida en el Sistema Internacional es el segundo (s)
- Frecuencia (f): Se trata del número de veces que se repite una oscilación en un segundo. Su unidad de medida en el Sistema Internacional es el hertzio (Hz)
En el caso de la bola del ejemplo anterior, el periodo es el tiempo que tarda esta en volver a pasar por el mismo punto en igual sentido. La frecuencia es el número de veces en un segundo en que la bola pasa por el mismo punto en igual sentido.
El periodo y la frecuencia son magnitudes inversas:
Con esto tenemos que 1 Hz = 1 s-1
Aunque el concepto de vibración es el mismo que el de oscilación, en ocasiones se emplea el término vibración para designar una oscilación muy rápida o de alta frecuencia.
Tipos de vibraciones
Existen dos tipos de vibraciones u oscilaciones atendiendo a las fuerzas que actúan:
- Oscilaciones libres: Cuando sobre el cuerpo no actúan fuerzas disipativas. El cuerpo no se detiene, oscila indefinidamente, al no haber una fuerza que contrarreste el efecto de la fuerza restauradora
- Oscilaciones amortiguadas: Cuando actúan fuerzas disipativas (como por ejemplo la fuerza de rozamiento o de fricción) que acaban por hacer que las oscilaciones desaparezcan. El cuerpo acabará retornando a la posición de equilibrio
El Movimiento Armónico Simple: Características
Cuando las fuerzas restauradoras que actúan sobre la partícula son proporcionales a la distancia al punto de equilibrio, decimos que se produce un movimiento armónico simple (m.a.s), también conocido comomovimiento vibratorio armónico simple (m.v.a.s.). En general, dichas fuerzas restauradoras siguen la ley de Hooke:
Una partícula o sistema tiene movimiento armónico simple (m.a.s.) cuando vibra bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio.
La bola del experimenta y aprende anterior es un movimiento armónico simple pues, como puede observarse, la fuerza restauradora, en rojo, es proporcional a la distancia al punto de equilibrio.
Características del movimiento armónico simple:
- Vibratorio: El cuerpo oscila en torno a una posición de equilibrio siempre en el mismo plano
- Periódico: El movimiento se repite cada cierto tiempo denominado periodo (T). Es decir, el cuerpo vuelve a tener las mismas magnitudes cinemáticas y dinámicas cada T segundos
- Se describe mediante una función sinusoidal (seno o coseno indistintamente)
A la partícula o sistema que se mueve según un movimiento armónico simple se les denomina oscilador armónico.
Magnitudes del movimiento armónico simple
- Elongación, x: Representa la posición de la partícula que oscila en función del tiempo y es la separación del cuerpo de la posición de equilibrio. Su unidad de medidas en el Sistema Internacional es el metro (m)
- Amplitud, A: Elongación máxima. Su unidad de medidas en el Sistema Internacional es el metro (m).
- Frecuencia. f: El número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.
- Periodo, T: El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
- Fase,
φ : La fase del movimiento en cualquier instante. Corresponde con el valorφ=ω⋅t+φ0 . Se trata del ángulo que representa el estado de vibración del cuerpo en un instante determinado. Su unidad de medida en el Sistema Internacional es el radián (rad). Cuando se produce una oscilación completa, la fase aumenta en 2·π radianes y el cuerpo vuelve a su posición (elongación) x inicial. Esto es debido a quecos(φ)=cos(φ+2⋅π) - Fase inicial,
φ0 : Se trata del ángulo que representa el estado inicial de vibración, es decir, la elongaciónx del cuerpo en el instante t = 0. Su unidad de medida en el Sistema Internacional es el radián (rad) - Frecuencia angular, velocidad angular o pulsación,
ω : Representa la velocidad de cambio de la fase del movimiento. Se trata del número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Su relación con el período y la frecuencia esω=2⋅πT=2⋅π⋅f
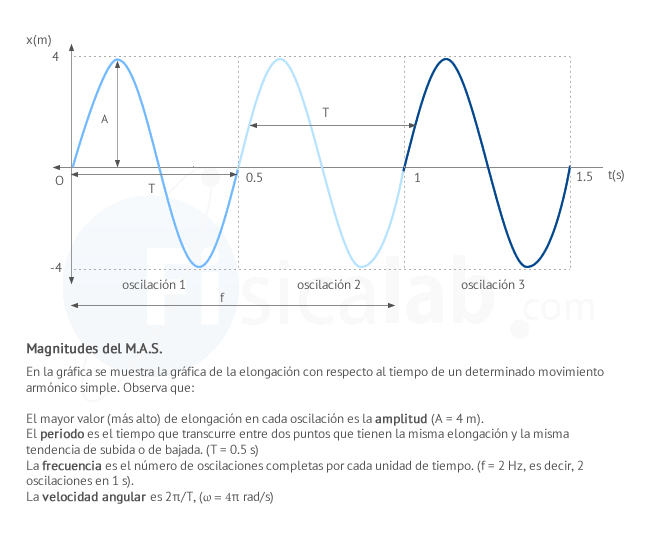
Gráfica de posición en el movimiento armónico simple (m.a.s.)
No es casualidad que el movimiento armónico simple se denomine, precisamente, armónico. También las funciones seno y coseno suelen denominarse funciones armónicas.
La gráfica de la elongación del movimiento armónico simple es la de una función sinusoidal cuya variable independiente es el tiempo.
Algunos casos de movimiento armónico simple
Es frecuente estudiar algunos elementos que se comportan como osciladores armónicos para entender las propiedades y características del m.a.s. con mayor profundidad. En este tema vamos a estudiar:
- El m.a.s. en muelles
- El m.a.s. en péndulos
- El movimiento armónico simple en el movimiento circular uniforme
Recuerdo de trigonometría...
Existen algunas relaciones trigonométricas que es importante que recuerdes y que te serán útiles cuando resuelvas ejercicios de este tema:
Los muelles están presentes en una gran y variada cantidad de objetos que te rodean: colchones, pesos, automóviles, bicicletas. En este apartado veremos:
- Si los muelles son considerados osciladores armónicos
- Qué ocurre cuando cuelgas un cuerpo de un muelle vertical
¿Son los muelles osciladores armónicos?
Un oscilador armónico es cualquier partícula o sistema que se mueve según un movimiento armónico simple.
Los muelles se comportan como osciladores armónicos cuando los apartamos de su posición de equilibrio. La fuerza elástica o restauradora del muelle es la responsable del movimiento vibratorio, una vez que el muelle se ha apartado de su posición de equilibrio.
Comprobación en cuerpo suspendido por muelle
En un oscilador armónico existe una posición de equilibrio estático. Cuando la partícula se separa de dicha posición de equilibrio aparece una fuerza proporcional a la distancia de separación. Para comprobar si un muelle se comporta como un oscilador armónico podemos distinguir dos casos típicos:
- Muelle vertical desde el que se cuelga un cuerpo. En él intervienen dos fuerzas, la fuerza elástica Fe , que sigue la ley de Hooke, y el peso P
- Muelle horizontal unido a un cuerpo. En este caso sólo interviene una fuerza, la fuerza elástica Fe
Dado que el segundo caso es una simplificación del primero en el que la fuerza total es directamente Fe, vamos a comprobar que, en el primero de los casos, el cuerpo efectivamente se comporta como un oscilador armónico.
Partimos de un muelle de constante elástica k, cuya posición de equilibrio es L0, desde el que cuelga una partícula de masa m. Al colgar la partícula, la posición de equilibrio pasa a ser l0 = L0 + x0. Recuerda que la fuerza elástica en un muelle sigue la ley de Hooke.
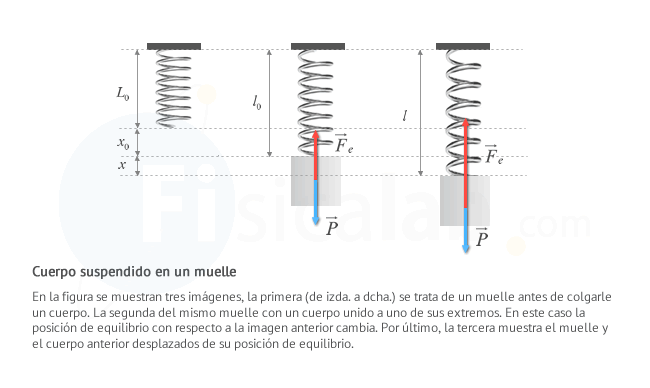
- En equilibrio
- La partícula unida al muelle no tiene aceleración. Por tanto, la fuerza resultante que actúa sobre la partícula
F⃗ t=0
- Si tiras del muelle hacia abajo y sueltas
- La fuerza elástica crece de manera proporcional a la distancia de separación a la posición de equilibrio.
Fe=−k⋅(x0+x) . Observa que al crecer, su valor ahora será mayor que el del peso - Por ello, la fuerza resultante
F⃗ t=F⃗ e+P⃗ ≠0 ,lo que hace que aparezca una aceleración que trata de devolver al muelle a su posición original de equilibrioConsiderando el sentido positivo hacia abajo y que, tal y como habíamos visto,k⋅x0=m⋅g ,nos queda:
Observa la similitud que tiene la expresiónFt=−k⋅x con la ley de Hooke, pero ten en cuenta que x es la distancia a la posición que tiene el cuerpo cuando se cuelga del muelle y no, directamente, a la posición de equilibrio del propio muelle sin objeto colgado L0 .La fuerza total que actúa sobre un objeto cuando cuelga de un muelle tiene igual valor que la fuerza elástica de un hipotético muelle cuya posición de equilibrio fuese L0 + x0 y por tanto x su distancia a la posición de equilibrio.Teniendo en cuenta el principio fundamental o Segunda Ley de Newton, podemos calcular la aceleración del cuerpo en cada punto de su oscilación:
- La fuerza elástica crece de manera proporcional a la distancia de separación a la posición de equilibrio.
- Cuando el muelle vuelve a pasar por la posición de equilibrio x0 lo hace con cierta velocidad. Una vez cruzada dicha posición la aceleración que actúa sobre la partícula cambia de sentido haciendo que la velocidad disminuya su módulo hasta detenerse en el extremo contrario al punto en que se inició el movimiento.
- El proceso se repite como si nos encontráramos de nuevo en el punto 2. Ten en cuenta que si no existiese rozamiento, el muelle nunca pararía.
En el siguiente experimenta y aprende tienes un muelle. Estíralo o comprímelo y súeltalo para observar como la partícula sigue un movimiento armónico simple. Concretamente, la distancia a la posición de equilibrio varía en forma de sinusoide con el paso del tiempo.
El péndulo simple se puede considerar un caso de movimiento armónico simple (m.a.s.), cuando se cumplen ciertas condiciones que veremos en este apartado. Aprenderemos:
- Qué es un péndulo simple
- Las fuerzas que intervienen en el movimiento del péndulo
- Bajo qué condiciones se puede considerar el péndulo un m.a.s.
- De qué depende el periodo del péndulo
También puedes:
- Tener una visión general sobre el movimiento armónico simple y sus magnitudes
Concepto de péndulo simple
Un péndulo simple es una masa puntual m suspendida verticalmente mediante una cuerda o hilo inextensible de masa despreciable y longitud l
Nos interesa conocer si podemos aplicar los conceptos propios del m.a.s. al estudio del péndulo. Recuerda que una partícula o sistema tiene movimiento armónico simple (m.a.s) cuando oscila bajo la acción de fuerzas restauradoras que son proporcionales a la distancia respecto a la posición de equilibrio.
¿Cómo se comportan los péndulos?
Cuando el péndulo se encuentra en reposo, en vertical, permanece en equilibrio ya que la fuerza peso es contrarrestada por la tensión en la cuerda.
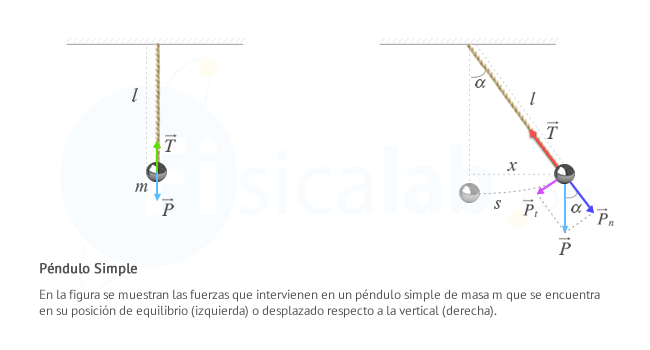
Cuando se separa de la posición de equilibrio la tensión contrarresta solo a la componente normal del peso, siendo la componente tangencial del peso la fuerza resultante. Esta fuerza es la responsable de que aparezca una aceleración ( F = m · a ) que trata de devolver al péndulo a su posición de equilibrio.
Componentes tangencial y normal de una fuerza
Es posible que no recuerdes con claridad qué es la componente tangencial y normal de una fuerza, también llamadas componentes intrínsecas. Para definirlas utilizamos un sistema de referencia intrínseco en cada punto de la trayectoria, tal y como se puede ver en la figura.
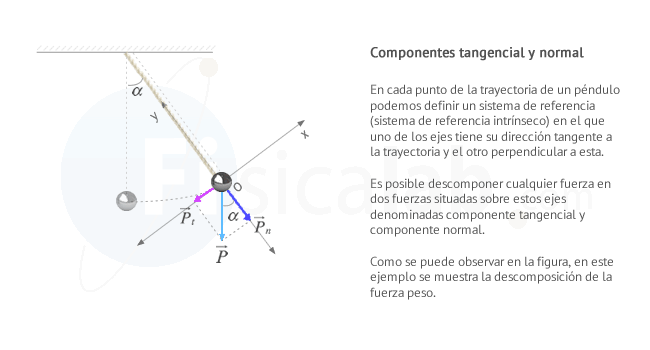
Es importante que Observes que el sistema de referencia se establece para cada punto de la trayectoria: Uno de los ejes es tangente a la trayectoria en ese punto. El otro es perpendicular al primero, es decir, normal a la trayectoria en ese punto.
Una vez establecidos los ejes en cada punto de la trayectoria podemos descomponer las fuerzas en estos ejes:
- Componente tangencial: Es la proyección de la fuerza sobre el eje tangente
- Componente normal: Es la proyección de la fuerza sobre el eje normal
El péndulo simple como oscilador armónico
Un péndulo simple se comporta como un oscilador armónico cuando oscila con amplitudes pequeñas. La fuerza restauradora es la componente tangencial del peso, de valor Pt, y la aceleración del péndulo es proporcional al desplazamiento pero de sentido contrario, con expresión:
Donde:
- a: Aceleración del péndulo. Depende de la distancia a la posición de equilibrio x. Su unidad de medida en el Sistema Internacional es el metro por segundo al cuadrado ( m/s2 )
- g: Aceleración de la gravedad. Su valor es 9.8 m/s2
- l: Longitud del péndulo. Su unidad de medida en el Sistema Internacional es el metro ( m )
- x: Separación x de la vertical de equilibrio del péndulo. Su unidad de medida en el Sistema Internacional es el metro ( m )
Comprobación
Un oscilador armónico no es más que una partícula que se mueve según un m.a.s. La aceleración que aparece en el péndulo cuando se separa de su posición de equilibrio hace que el péndulo vibre u oscile en torno a suposición de equilibrio. Dichas vibraciones siguen el patrón de un movimiento armónico simple si el ángulo de oscilación es pequeño (no más de 15º o 20º). Esto implica que:
sin(α)≅α - La longitud de la trayectoria curva s y el desplazamiento x en el eje horizontal tienden a igualarse
- La aceleración normal es despreciable
- Se puede considerar que la trayectoria del móvil es horizontal
- La posición viene dada por la separación x a la vértical de equilibrio
Con lo anterior nos queda:
Con lo que podemos afirmar que la aceleración es proporcional al desplazamiento pero de sentido contrario, siendo
Periodo del péndulo simple
El periodo del péndulo simple, para oscilaciones de poca amplitud, viene determinado por la longitud del mismo y la gravedad. No influye la masa del cuerpo que oscila ni la amplitud de la oscilación.
El periodo del péndulo simple es el tiempo que tarda el péndulo en volver a pasar por un punto en el mismo sentido. También se define como el tiempo que tarda en hacerse una oscilación completa. Su valor viene determinado por:
Donde:
- T: Periodo del péndulo. Su unidad de medida en el Sistema Internacional es el segundo ( s )
- l: Longitud del péndulo. Su unidad de medida en el Sistema Internacional es el metro ( m )
- g: Gravedad. Su unidad de medida en el Sistema Internacional es el metro por segundo al cuadrado ( m/s2 )
¿Cómo determinar el valor de la gravedad con un péndulo?
La expresión anterior nos permite calcular el periodo conocidas la longitud del péndulo y el valor de la gravedad. Siguiendo el proceso inverso podemos determinar el valor de la gravedad. Conocida la longitud l, medimos el tiempo que tarda el péndulo en realizar una oscilación completa y aplicamos la siguiente expresión, despejada de la expresión del periodo anterior:
Para ver un desarrollo de la obtención de la anterior expresión, visita el apartado de dinámica del movimiento armónico simple.
Cuando una partícula se mueve según un movimiento armónico simple (m.a.s) aparecen las mismas magnitudes cinemáticas que en cualquier tipo de movimiento, es decir, la posición, la velocidad y la aceleración. En este apartado veremos:
- La posición y la gráfica de posición - tiempo en un oscilador armónico
- Su velocidad y su gráfica de velocidad - tiempo
- La aceleración del m.a.s. y la gráfica aceleración - tiempo
- Graficamente, la relación que guardan las magnitudes cinemáticas entre sí
Adicionalmente, puede que te interese conocer:
- El concepto de movimiento armónico simple u oscilador armónico
No olvides que dichas magnitudes son, en general, magnitudes vectoriales. Sin embargo, en este apartado, dado que el m.a.s. se desarrolla en una sola dimensión, podremos utilizar el convenio de signos en movimientos rectilíneos habitual.
Posición
La posición de una partícula que sigue un movimiento armónico simple ( m.a.s.), también denominadaelongación, viene determinada por la distancia x a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m). Se trata de una función sinusoidal (seno o coseno), que depende del tiempo x =f(t).
Ecuación de posición
| x → Seno | x → Coseno | |
| Con | ||
| Conf | ||
| ConT |
Donde:
- A: Amplitud máxima del movimiento. Representa la distancia máxima a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)
- f: Frecuencia del movimiento. Es el número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación /segundo = 1 s-1.
- T: Periodo del movimiento. El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
ω : Frecuencia angular o pulsación. Representa el número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Se encuentra relacionada con la frecuencia y el periodo del movimiento segúnω=2⋅πT=2⋅π⋅f φ0 yφ'0 : Fase inicial. Se trata del ángulo que representa el estado inicial de vibración, es decir, la posición x del cuerpo en el instante t = 0. Su valor depende de si has elegido un seno o un coseno para representar el movimiento.φ'0=φ0−π/2 Su unidad de medida en el Sistema Internacional es el radián (rad) .
Para cualquier instante t se cumple que x(t)=x(t+T) .
Gráfica de posición x - t

Velocidad
La velocidad instantánea determina la variación de posición que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la posición respecto al tiempo.
Para obtener la expresión de la velocidad hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno:
v=ddt(A⋅sin(ω⋅t+φ0))=A⋅ω⋅cos(ω⋅t+φ0) v=ddt(A⋅cos(ω⋅t+φ'0))=−A⋅ω⋅sin(ω⋅t+φ'0)
Ecuación de velocidad
Velocidad
(cuando x → Seno ) | Velocidad (cuando x → Coseno ) | |
| Con | ||
| Conf | ||
| ConT |
Para cualquier instante t se cumple que v(t)=v(t+T) .
Gráfica de velocidad v - t

La velocidad es máxima cuando el cuerpo pasa por la posición de equilibrio y mínima en los extremos de latrayectoria del movimiento (+A y -A).
Relación posición - velocidad (x - v)
Podemos relacionar la posición y la velocidad en un movimiento armónico simple a través de la expresión:
Comprobación
La idea principal es poder hacer uso de la relación trigonométrica: sin2(α)+cos2(α)=1
Aceleración
La aceleración instantánea determina la variación de velocidad que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la velocidad respecto al tiempo.
Para obtener la expresión de la aceleración hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno:
a=d2dt2(A⋅sin(ω⋅t+φ0))=ddt(A⋅ω⋅cos(ω⋅t+φ0))=−A⋅ω2⋅sin(ω⋅t+φ0) a=d2dt2(A⋅cos(ω⋅t+φ'0))=ddt(−A⋅ω⋅sin(ω⋅t+φ'0))=−A⋅ω2⋅cos(ω⋅t+φ'0)
Ecuación de aceleración
| Aceleración (cuando x → Seno ) | Aceleración (cuando x → Coseno ) | |
| Con | ||
| Conf | ||
| ConT |
Para cualquier instante t se cumple que a(t)=a(t+T) .
Gráfica de aceleración a - t

La aceleración es máxima en los extremos de la trayectoria (+A y -A) y mínima cuando el cuerpo pasa por la posición de equilibrio.
Relación posición - aceleración (x - a)
Podemos relacionar la posición y la aceleración en un movimiento armónico simple a través de la expresión:
Comprobación
Para deducir la fórmula que relaciona posición y aceleración, simplemente tenemos que percatarnos que podemos obtener la expresión de la aceleración a=−A⋅ω2⋅sin(ω⋅t+φ0) multiplicando la expresión de la posición x=A⋅sin(ω⋅t+φ0) por un factor de −ω2
No hay comentarios.:
Publicar un comentario