Electricidad

Desde que los griegos descubrieron las curiosas propiedades del ámbar al ser frotado, hasta los actuales nanoconductores, el estudio de la electricidad ha ocupado algunas de las mentes más lúcidas de la humanidad.

La electrostática es la rama de la Física que estudia las interacciones entre cuerpos cargados eléctrica mente que se encuentran en reposo. En este tema estudiaremos los fundamentos y leyes que gobiernan la electricidad y descubriremos que la carga eléctrica es una propiedad intrínseca de la materia, al igual que lo es la masa. Esto nos permitirá, en temas posteriores, estudiar qué ocurre cuando las cargas se encuentran en movimiento.

Para enfrentarte a este tema, te recomendamos que manejes con soltura los vectores.

Breve Introducción

¿Has probado a frotar un bolígrafo de plástico en un jersey de lana y acercarlo a un grupo de pequeños papeles? Si no lo has hecho todavía podrás comprobar que los trocitos de papel son atraídos por tu bolígrafo e incluso algunos pueden quedar suspendidos en él.

Esta fuerza de atracción capaz de vencer la fuerza de la gravedad, denominada fuerza eléctrica, es y ha sido objeto de estudio por numerosos científicos a lo largo de la historia.

Y es que esta capacidad que poseen algunos objetos al ser rozados, ya era conocida por los antiguos griegos. En concreto, Tales de Mileto (s. VII a.C.) comprobó que al frotar ciertos cuerpos con un paño aparecían ciertas fuerzas "inexplicables" y que eran mucho más intensas en el ámbar, en griego, elektron.

Sin embargo, no se comienza a comprender estos fenómenos hasta la llegada del Renacimiento. A principios del siglo XVII, William Gilbert (1554-1603) descubrió numerosos materiales que poseían un comportamiento similar al ámbar, a los que llamó "eléctricos". Basándose en este hecho, estableció una clasificación que diferenciaba entre sustancias eléctricas y no eléctricas. Años más tarde, dicha clasificación fué rechazada por Charles François de Cisternay du Fay (1698-1739), quién descubrió que existen dos tipos de electricidad estableciendo la teoría del doble fluido eléctrico: vítreo (opuesto al ámbar) o resinoso (como el ámbar).

Por otro lado Benjamin Franklin (1706-1790), en el siglo XVIII estableció que la electricidad era un fluido que puede encontrarse en exceso (carga positiva) o en defecto (carga negativa), estableciendo así lo que se conoce como la teoría del fluido eléctrico único. Sin embargo en ese mismo siglo, Michael Faraday (1791-1867), determinó que Franklin estaba parcialmente equivocado y que la electricidad no se trataba de un fluido si no de partículas con carga. Esa carga fué bautizada por el físico George Johnstone Stoney (1826-1911) como electrón(en honor al ámbar), aunque no sería hasta 1897 cuando Joseph John Thomson (1856-1940) lo descubre por medio de una serie de experimentos con rayos catódicos. Posteriormente, Ernest Rutherford encontró otra partícula subatómica con carga opuesta al electrón que llamó protón.

Hoy en día sabemos que la materia es intrínsecamente eléctrica porque las partículas que componen los átomos poseen esta propiedad.

¿Qué es la carga eléctrica?

En la física moderna, la carga eléctrica es una propiedad intrínseca de la materia responsable de producir las interacciones electrostáticas.

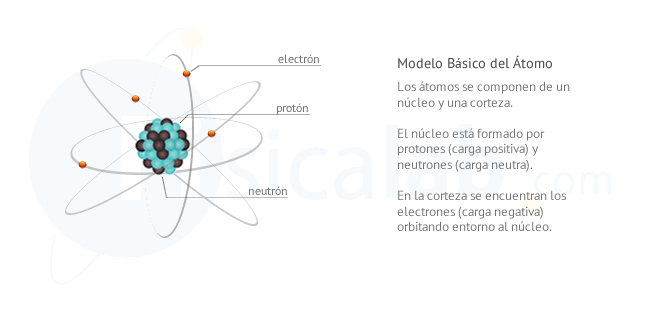
En la actualidad no se sabe qué es o por qué se origina dicha carga, lo que si se conoce es que la materia ordinaria se compone de átomos y estos a su vez se componen de otras partículas llamadas protones (p+) y electrones (e-). Los primeros se encuentran en lo que se denomina núcleo del átomo y los segundos, en lo que se denomina corteza, girando entorno al núcleo. Dado que se encuentran en la periferia, estos se fugan (se pierden) o ingresan (se ganan) con facilidad.

Al igual que existen dos tipos de electrización (atractiva y repulsiva), existen dos tipos de carga (positiva y negativa). Los electrones poseen carga negativa y los protones positiva, aunque son idénticas en valor absoluto. Robert Millikan, en 1909 pudo medir el valor de dicha carga, simbolizado con la letra e, estableciendo que:

 e = 1.602 · 10-19 culombios

Propiedades de la carga eléctrica

1. Dado que la materia se compone de protones y electrones, y su carga es e, podemos deducir que la carga eléctrica es una magnitud cuantizada, o lo que es lo mismo, la carga eléctrica de cualquier cuerpo es siempre un múltiplo del valor de e.

2. En cualquier caso, la carga eléctrica de un cuerpo se dice que es:

• Negativa, cuando tiene más electrones que protones.
• Positiva, cuando tiene menos electrones que protones.
• Neutra, cuando tiene igual número de electrones que de protones.

3. En cualquier fenómeno físico, la carga del sistema que estemos estudiando es idéntica antes y después de que ocurra el fenómeno físico, aunque se encuentre distribuida de otra forma. Esto constituye lo que se conoce como el principio de conservación de la carga: La carga ni se crea ni se destruye ya que su valor permanece constante.

4. Las cargas pueden circular libremente por la superficie de determinados cuerpos. Aquellos que permiten dicho movimiento reciben el nombre conductores y aquellos que no lo permiten se denominan aislantes.

5. La fuerza de atracción o repulsión entre dos cargas, tal y como establece la ley de Coulomb, depende del inverso del cuadrado de la distancia que los separa.

Fuerza Eléctrica

En 1785, Charles Augustin de Coulomb (1736-1806), físico e ingeniero francés que también enunció las leyes sobre el rozamiento, presentó en la Academia de Ciencias de París, una memoria en la que se recogían sus experimentos realizados sobre cuerpos cargados, y cuyas conclusiones se pueden resumir en los siguientes puntos:

• Los cuerpos cargados sufren una fuerza de atracción o repulsión al aproximarse.
• El valor de dicha fuerza es proporcional al producto del valor de sus cargas.
• La fuerza es de atracción si las cargas son de signo opuesto y de repulsión si son del mismo signo.
• La fuerza es inversamente proporcional al cuadrado de la distancia que los separa.

Estas conclusiones constituyen lo que se conoce hoy en día como la ley de Coulomb.

La fuerza eléctrica con la que se atraen o repelen dos cargas puntuales en reposo es directamente proporcional al producto de las mismas, inversamente proporcional al cuadrado de la distancia que las separa y actúa en la dirección de la recta que las une.

F=K⋅Q⋅qr2

donde:

• F es la fuerza eléctrica de atracción o repulsión. En el S.I. se mide en Newtons (N).
• Q y q son lo valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
• r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
• K es una constante de proporcionalidad llamada constante de la ley de Coulomb. No se trata de una constante universal y depende del medio en el que se encuentren las cargas. En concreto para el vacío k es aproximadamente 9·109 N·m2/C2 utilizando unidades en el S.I.

Si te fijas bien, te darás cuenta que si incluyes el signo en los valores de las cargas, el valor de la fuerza eléctrica en esta expresión puede venir acompañada de un signo. Este signo será:

• positivo. cuando la fuerza sea de repulsión (las cargas se repelen).  ( + · + = + o - · - = + )
• negativo. cuando la fuerza sea de atracción (las cargas se atraen). ( + · - = - o - · + = - )

Por tanto, si te indican que dos cargas se atraen con una fuerza de 5 N, no olvides que en realidad la fuerza es  -5 N, porque las cargas se atraen.

Expresión vectorial de la fuerza eléctrica

La fuerza eléctrica descrita en la ley de Coulomb no deja de ser una fuerza y como tal, se trata de unamagnitud vectorial que en el Sistema Internacional de Unidades se mide en Newtons (N). Su expresión en forma vectorial es la siguiente:

F⃗ =K⋅Q⋅qr2⋅u⃗ r

donde el nuevo valor u⃗ r es un vector unitario en la dirección que une ambas cargas. Observa que si llamamos r⃗  al vector que va desde la carga que ejerce la fuerza hacia la que la sufre, u⃗ r es un vector que nos indica la dirección de r⃗ 

u⃗ r=r⃗ r/

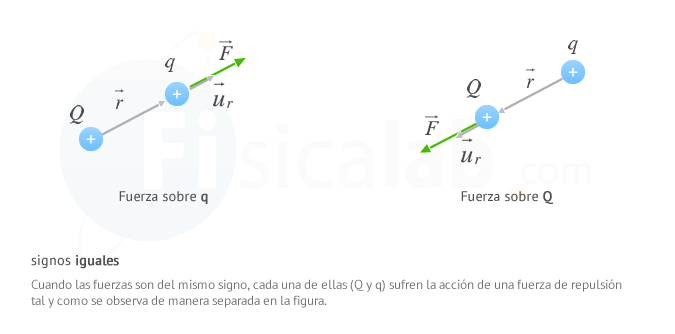
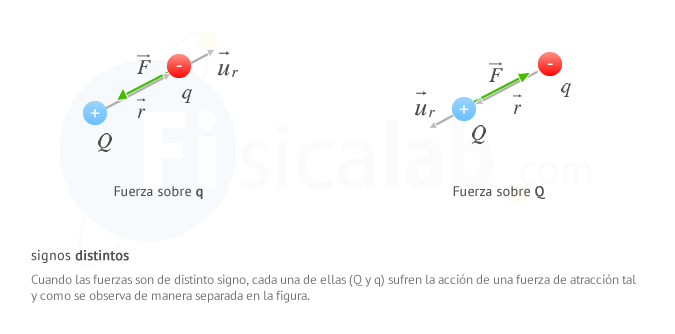
Date cuenta que la fuerza electrica siempre tiene la misma dirEn el Sistema Internacional de Unidades (S.I.) la carga eléctrica (q) es una magnitud derivada cuyo unidad recibe el nombre de culombio (C), en honor al físico francés Charles-Augustin de Coulomb. Para definirla se hace uso de la intensidad de corriente eléctrica que es una magnitud fundamental en el S.I. y cuya unidad es el amperio (A). De esta forma:

Un culombio (C) es la cantidad de carga eléctrica que atraviesa cada segundo (s) la sección de un conductor por el que circula una corriente eléctrica de un amperio (A).

1 C = 1 A⋅s

Un culombio es una unidad de carga muy grande por lo que es común utilizar submúltiplos de esta. A continuación puedes encontrar algunos de los más utilizados:

• Miliculombio. 1 mC = 10-3 C
• Microculombio. 1 µC = 10-6 C
• Nanoculombio. 1 nC = 10-9 C
• Picoculombio. 1 pC = 10-12 C 

ección que el vector unitario u⃗ r y el mismo sentido si tienen el mismo signo y sentido opuesto si tienen signo distinto.

Principio de Superposición

La ley de Coulomb determina la fuerza eléctrica de atracción o repulsión que experimenta un carga puntual ante la presencia de otra. Sin embargo, ¿qué ocurre si deseamos conocer dicha fuerza cuando nuestra carga se encuentra rodeada de más de una carga?. La respuesta es bien sencilla, al igual que hacíamos con la suma de fuerzas en los apartados de las leyes de Newton, aplicaremos lo que se conoce como principio de superposición:

La fuerza neta que actúa sobre cada carga será la fuerza resultante que sobre ella ejercen el resto de cargas.

o lo que es lo mismo:

Si disponemos de n cargas, q1, q2, ..., qn, la fuerza neta que actúa sobre una de las cargas de un sistema de cargas es la suma vectorial de las fuerzas que el resto de cargas ejercen por separado sobre ella. Por ejemplo, la fuerza que actúa sobre la carga q1 será:

F⃗ 1=F⃗ 2,1+F⃗ 3,1+...+F⃗ n,1

donde:

• F1 es la fuerza eléctrica que actúa sobre la carga q1
• F2,1 es la fuerza que provoca la carga q2 sobre q1.
• ...
• Fn,1 es la fuerza que provoca la carga qn sobre q1.

Trabajo Eléctrico

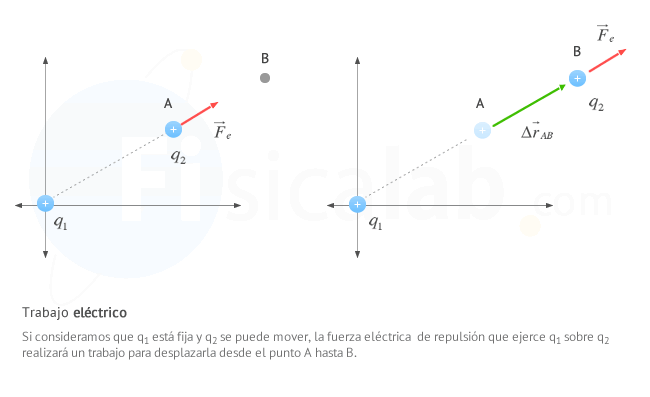
Como hemos estudiado anteriormente, si aplicas una fuerza sobre una caja y esta se desplaza, decimos que la fuerza que ejercemos realiza un trabajo. De igual forma, si un cuerpo que se encuentra cargado ejerce unafuerza eléctrica de atracción o repulsión sobre otro que también se encuentre cargado, dicha fuerza realizará un trabajo mientras este último se desplace.

El trabajo eléctrico es el trabajo que realiza una fuerza eléctrica sobre una carga que se desplaza desde un punto A hasta otro punto B.

Si suponemos que la fuerza es constante durante todo el desplazamiento, se puede expresar de la siguiente forma:

W⃗ e(A→B)=F⃗ e⋅Δr⃗ AB

donde:

• W⃗ e(A→B) es el trabajo eléctrico. En el S.I. se mide en Julios (J).
• F⃗ e es la Fuerza eléctrica que sufre la carga. En el S.I. se mide en Newtons (N).
• Δr⃗ AB es el vector desplazamiento entre ambos puntos. En el S.I. se mide en metros (m).

Al igual que ocurre con otras fuerzas, como la fuerza gravitatoria, la fuerza eléctrica es una fuerza conservativa. Esto implica que:

• El trabajo que realiza una fuerza eléctrica para mover un cuerpo cargado desde una posición A hasta otra B, únicamente depende de dichas posiciones y no del camino seguido para llegar de A a B.
• Cuando el camino que sigue el cuerpo entre A y B es un camino cerrado o un ciclo, el trabajo eléctrico es nulo.

Signo del Trabajo Eléctrico

Si nos atenemos a la expresión matemática de trabajo eléctrico, nos damos cuenta de que la operación principal es un producto escalar. Esta operación puede devolver un valor positivo, negativo o nulo, dependiendo del menor ángulo que se forme entre la fuerza eléctrica y el vector desplazamiento. Si el ángulo (α) es:

• α > 90º. El trabajo eléctrico será negativo (We < 0).
• α = 90º. El trabajo eléctrico será nulo (We = 0).
• α < 90º. El trabajo eléctrico será positivo (We > 0).

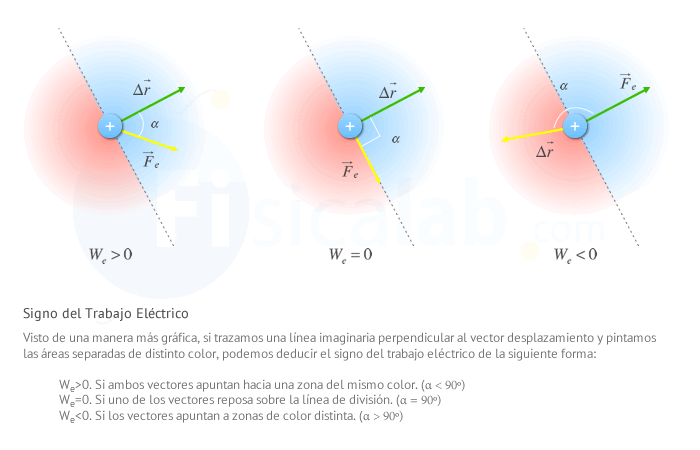
¿Cómo podemos interpretar este signo?. A priori, si un cuerpo cargado se encuentra libre y derrepente sufre la acción de una fuerza eléctrica, el cuerpo se moverá en el sentido de la fuerza eléctrica y por tanto, el trabajo eléctrico será positivo. 

Si por el contrario, se le aplica una fuerza externa contraria a la fuerza eléctrica que provoca un desplazamiento opuesto al que debería producir la fuerza eléctrica, el trabajo eléctrico será un valor negativo.

El trabajo eléctrico de una fuerza eléctrica siempre será positivo salvo que intervenga alguna fuerza externa que provoque un desplazamiento opuesto al que debería provocar únicamente la fuerza eléctrica.

Trabajo de Fuerzas Externas contrarias a la Fuerza Eléctrica

El trabajo eléctrico es el trabajo que realizan las fuerzas eléctricas, pero ¡no te confundas!. Otra cosa distinta es el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). En este caso, el trabajo realizado por dicha fuerza externa para mover un cuerpo desde un punto A a otro B es:

We=−Wf

donde:

• We es el trabajo realizado por la fuerza eléctrica para moverlo desde A hasta B.
• Wf es el trabajo realizado por la fuerza externa para moverlo desde A hasta B.

Energía Potencial Eléctrica

Cuando hablamos de la energía potencial gravitatoria estudiamos que un cuerpo que se encuentra a determinada altura de la superficie de la Tierra adquiere una determinada cantidad de energía potencial provocada por la acción de la fuerza gravitatoria. De igual forma, un cuerpo cargado que sufre la acción de unafuerza eléctrica adquiere energía potencial electrostática.

La energía potencial eléctrica que posee una carga puntual q1 en presencia de otra carga puntual q2 que se encuentran separadas cierta distancia es

Ep=K⋅q1⋅q2r 

donde:

• Ep es la energía potencial eléctrica. En el S.I. se mide en Julios (J).
• q1 y q2 son los valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
• r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
• K es la constante de la ley de Coulomb. Para el vacío su valor es aproximadamente 9·109 N·m2/C2utilizando unidades en el S.I.

Date cuenta que la energía potencial eléctrica es:

• positiva si las cargas poseen el mismo signo y negativa si tienen signos distintos.
• nula cuando la distancia de separación es infinita.

Relación entre el trabajo eléctrico y la energía potencial eléctrica

Como ocurre con todas las fuerzas conservativas, existe una relación entre el trabajo eléctrico y la energía potencial eléctrica. En concreto, el trabajo que realiza una fuerza eléctrica para desplazar una carga desde un punto A hasta otro B puede expresarse de la siguiente forma:

We(A→B)=−(EpB − EpA) = EpA − EpB

o lo que es lo mismo:

We=−∆Ep 

Fuerzas Externas contrarias a la Fuerza Eléctrica

Como ya hablamos en el apartado de trabajo eléctrico, este es el trabajo que realizan las fuerzas eléctricas y no debemos confundirlo con el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). El trabajo que realiza dicha fuerza (Wf) se relaciona con el trabajo eléctrico (We) y la energía potencial eléctrica de la siguiente forma :

We=−Wf=−ΔEp

A continuación, vamos a estudiar que esta relación se cumple en los dos casos comentados anteriormente.

Cargas con distinto signo

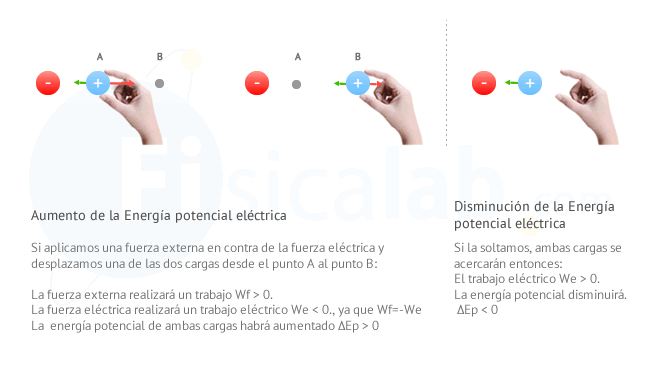
Imagina dos cargas fijas, una positiva y otra negativa. En principio, dado que se trata de cargas con distinto signo en cada una de ellas aparecerá una fuerza de atracción hacia la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más alejado. Al hacer esto:

• Si aplicas la definiciónde trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
• Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
• Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).

En resumidas cuentas, el trabajo que realiza la fuerza externa al alejarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de acercarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.

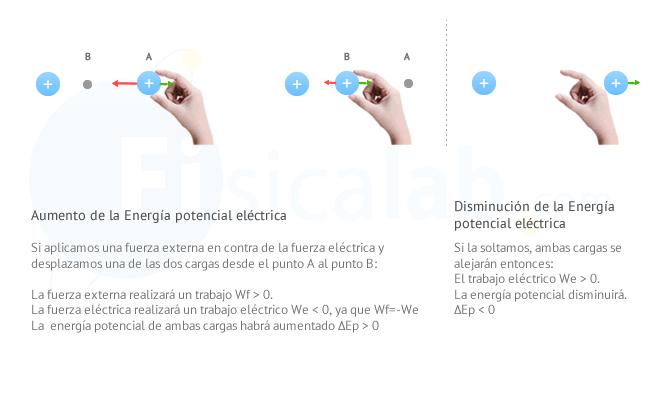
Cargas del mismo signo

Ahora, imagina dos cargas fijas del mismo signo (positiva o negativa). En principio, dado que se trata de cargas con signos iguales en cada una de ellas aparecerá una fuerza de repulsión en contra de la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más cercano. Al hacer esto, como en el caso anterior:

• Si aplicas la definiciónde trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
• Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
• Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).

El trabajo que realiza la fuerza externa al acercarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de alejarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.

Fíjate que tal y como indicamos en la fórmula inicial, cuando se aplica la fuerza externa, el signo del trabajo delcampo eléctrico es exactamente el contrario al del trabajo realizado por la fuerza eléctrica y al de la diferencia de energía potencial.

¿Qué es el Campo Eléctrico?

Tal y como establece la ley de Coulomb, la fuerza eléctrica es una fuerza a distancia. Si tenemos una carga positiva q y situamos próxima a ella otra carga positiva q', que llamaremos carga testigo, q' sufrirá de forma instantánea la acción de una fuerza eléctrica de repulsión que la obligará a moverse.

Si lo piensas bien, esto se cumple en todas las direcciones del espacio alrededor de la carga q, por tanto es lógico pensar que la propia carga crea un área de influencia donde hace notar su presencia independientemente de la carga testigo.

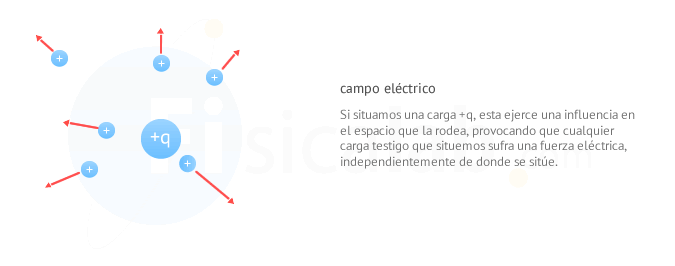
Para explicar la instantaneidad con la que se aplican las fuerzas a distancia y dicha área de influencia, el físico inglés Michael Faraday (1791-1867) introdujo el concepto de campo de fuerzas. En concreto, para el caso de la fuerza eléctrica:

Un campo eléctrico es la perturbación que genera una carga eléctrica en el espacio que la rodea, de tal forma que si introducimos una carga testigo en dicho campo actuará sobre ella una fuerza eléctrica.

Las magnitudes que describen a los campos eléctricos son:

• La intensidad del campo eléctrico en un punto

  Intensidad del Campo Eléctrico

  Para determinar la existencia o inexistencia de un determinado campo eléctrico, así como sus características, es necesario introducir dentro de él una carga q' que nos sirva de testeador. Esta carga q' se denomina carga de prueba o carga testigo y por convenio siempre se considera positiva.
  Si la carga testigo sufre la acción de una fuerza eléctrica, querrá decir que se encuentra en el seno de un campo eléctrico y gracias a ella podremos cuantificarlo por medio de una nueva magnitud denominada intensidad del campo eléctrico.
  La intensidad del campo eléctrico (E⃗ ) en un punto es una magnitud vectorial que representa la fuerza eléctrica(F⃗ ) que actúa por unidad de carga testigo positiva, q', situada en dicho punto.

  
  

  E⃗ =F⃗ q'

  La unidad de intensidad del campo eléctrico en el Sistema Internacional (S.I.) es el newton por culombio (N/C).
  Así, la intensidad del campo eléctrico, llamada más comunmente campo électrico (de forma simplificada), es un vector que tiene la misma dirección y sentido que la fuerza eléctrica que actúa sobre la carga testigo positiva. Además, su módulo se puede obtener mediante la siguiente expresión:
  
  

  E=Fq'

  Movimiento de Cargas en el Interior de un Campo Eléctrico

  Si partimos de la definición anterior, podemos determinar que la fuerza eléctrica que sufre una carga q situada en el interior de un campo eléctrico es:
  E⃗ =F⃗ q⇒F⃗ =q⋅E⃗ 
  
  
  De aquí podemos deducir que:
  • Si la carga es positiva (q > 0), la fuerza eléctrica tendrá el mismo signo que el campo y por tanto q se moverá en el sentido del campo.
  • Si la carga es negativa (q < 0), la fuerza eléctrica tendrá distinto signo que el campo y por tanto q se moverá en sentido contrario al campo.
  Las cargas positivas se mueven en el sentido del campo eléctrico y las cargas negativas se mueven en sentido contrario.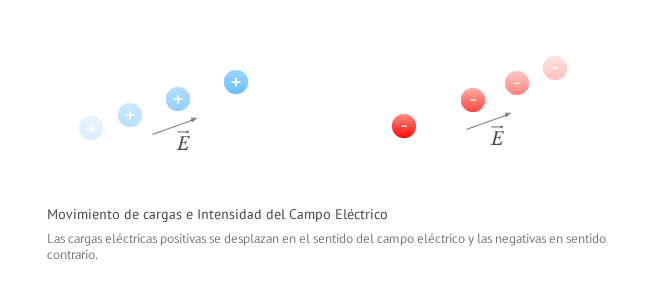
  

  Intensidad del Campo creado por una carga puntual

  Tal y como hemos visto anteriormente, en el caso de que deseemos calcular la intensidad del campo eléctrico en un determinado punto creado por una única carga puntual q, deberemos introducir una carga testigo positiva q' en dicho punto. A partir de aquí podemos emplear la ley de Coulomb (para calcular la fuerza electrica que sufre q') y la definición de intensidad del campo en un punto:
  E⃗ =F⃗ q'=K⋅q⋅q'r2⋅u⃗ rq'⇒E⃗ =K⋅qr2⋅u⃗ r
  
  
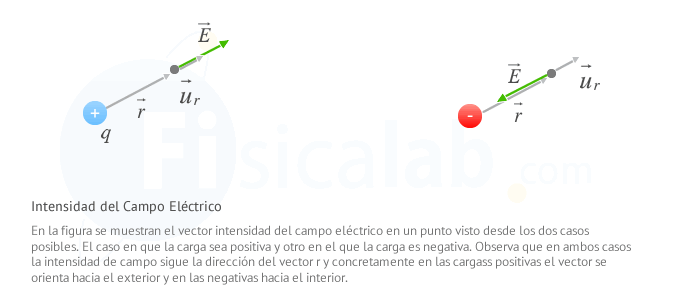
  La intensidad del campo eléctrico en un determinado punto creado por una carga puntual q se obtiene por medio de la siguiente expresión:

  
  

  E⃗ =K⋅qr2⋅u⃗ r

  donde:

  • E⃗  es la Intensidad del campo eléctrico en un punto.
  • K es la constante de la ley de Coulomb.
  • q es la carga que crea el campo.
  • r es el módulo del vector r⃗  que va desde la la carga q hasta el punto, o lo que es lo mismo, la distancia entre la carga y el punto donde se mide la intensidad.
  • u⃗ r es un vector unitario del vector r⃗ .
  
  Si analizamos la expresión podemos deducir las siguientes cuestiones:
  • La intensidad del campo eléctrico en un punto depende de la carga q que lo genera, la distancia entre dicha carga y dicho punto y el medio en el que se encuentren.
  • Cuanto mayor es la distancia entre la carga y el punto donde se mida, la intensidad del campo eléctrico será menor.
  • La intensidad del campo eléctrico no depende de la carga testigo q', que necesitamos introducir para medirlo, únicamente dependerá del valor de la carga que lo genera.
• El potencial eléctrico en un punto.

Para poder visualizar gráficamente el campo eléctrico, Michael Faraday (1791-1867) propuso una representación por medio de líneas denominadas líneas de campo o líneas de fuerza. Al trazar estas líneas debes tener en cuenta lo siguiente:

• Cada línea es una flecha cuya dirección y sentido es el de la fuerza eléctrica que actuaría sobre una carga testigo positiva. En cada punto de la línea la intensidad del campo eléctrico (E) es tangente en dicho punto.
• Las líneas no pueden cruzarse en ningún punto.
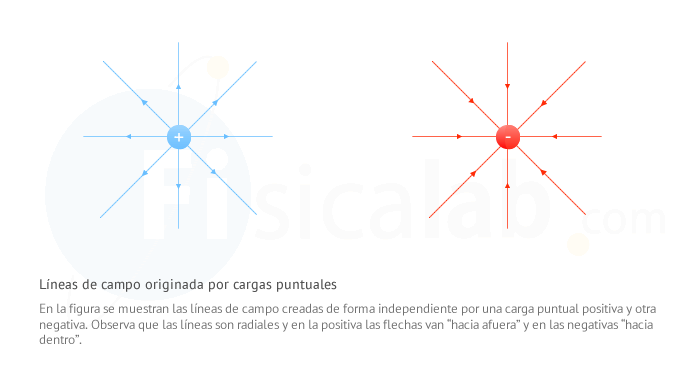
• Las líneas parten de las cargas positivas y entran en las cargas negativas, de ahí que a las cargas positivas se les denomine fuentes del campo y a las negativas sumideros.
• El número de líneas que salen o entran en la carga es proporcional al valor de esta.

• Cuanto más juntas estén las líneas, más intenso será el campo.
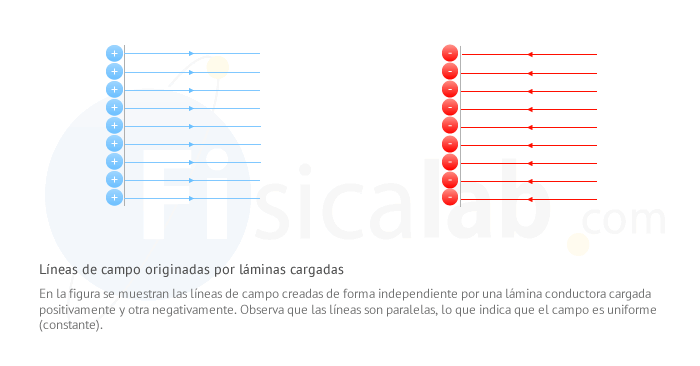
• En el caso en que la líneas de campo sean paralelas, el valor del campo eléctrico es constante.

Líneas de campo originadas por cargas puntuales

Líneas de campo originadas por conductores planos cargados

Líneas de campo originadas por dos cargas puntuales (dipolo)

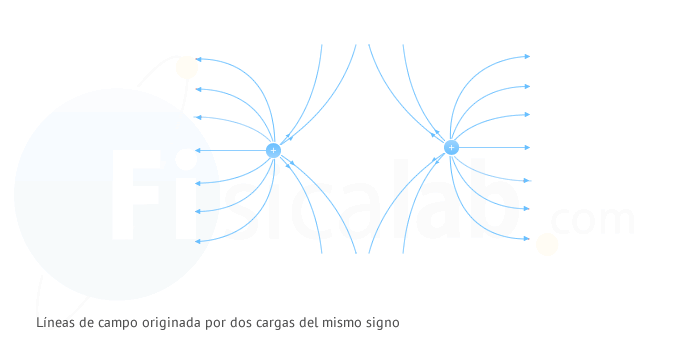
Si introducimos una carga q' en el seno de un campo eléctrico, la carga sufrirá la acción de una fuerza eléctrica y como consecuencia de esto, adquirirá cierta energía potencial eléctrica (también conocida como energía potencial electrostática). Si lo vemos desde una perspectiva más simple, podemos pensar que el campo eléctrico crea un área de influencia donde cada uno de sus puntos tienen la propiedad de poder conferir una energía potencial a cualquier carga que se sitúe en su interior.

A partir de este razonamiento, se establece una nueva magnitud escalar propia de los campos eléctricos denominada potencial eléctrico y que representa la energía potencial electrostática que adquiere una unidad de carga positiva si la situamos en dicho punto.

El potencial eléctrico en un punto del espacio de un campo eléctrico es la energía potencial eléctricaque adquiere una unidad de carga positiva situada en dicho punto.

V=Epq'

donde:

• V es el potencial eléctrico en un punto del campo eléctrico. Su unidad en el S.I. es el julio por culombio (J/C) que en honor a Alesandro Volta recibe el nombre de Voltio.
• Ep es la energía potencial eléctrica que adquiere una carga testigo positiva q' al situarla en ese punto.

El hecho de que todas las magnitudes sean escalares, permite que el estudio del campo eléctrico sea más sencillo. De esta forma, si conocemos el valor del potencial eléctrico V en un punto, podemos determinar que la energía potencial eléctrica de una carga q situada en él es:

Ep=V⋅q

Potencial eléctrico creado por una carga puntual

Tal y como estudiamos en el apartado de intensidad del campo eléctrico, una única carga q es capaz de crear un campo eléctrico a su alrededor. Si en dicho campo introducimos una carga testigo q' entonces, atendiendo a la definición de energía potencial eléctrica de dos cargas puntuales:

V=Epq'=K⋅q⋅q'rq'⇒V=K⋅qr

El potencial eléctrico del campo eléctrico creado por una carga puntual q se obtiene por medio de la siguiente expresión:

V=K⋅qr

donde:

• V es el potencial eléctrico en un punto.
• K es la constante de la ley de Coulomb.
• q es la carga puntual que crea el campo eléctrico.
• r es la distancia entre la carga y el punto donde medimos el potencial.

Si observas detenidamente la expresión puedes darte cuenta de que:

• Si la carga q es positiva, la energia potencial es positiva y el potencial eléctrico V es positivo.
• Si la carga q es negativa, la energía el potencial es negativa y el potencial eléctrico V es negativo.
• Si no existe carga, la energía potencial y el potencial eléctrico es nulo.
• El potencial eléctrico 

  Capacidad Eléctrica

  Si estudiamos detenidamente la expresión del potencial eléctrico creado por una carga puntual, puedes comprobar que a medida que la distancia se hace más pequeña (r→0) su valor V tiende al infinito (V→∞).
  
  

  V=K⋅qr
  Sin embargo en la vida cotidiana no disponemos de cargas aisladas, sino que generalmente las cargas se encuentran asociadas en conductores no puntuales, y esta condición no se cumple para ellos.
  
  En los conductores no puntuales la cargas se mueven libremente y se distribuyen de tal forma que la repulsión entre ellas se hace mínima, dejando que el exceso de carga se concentre únicamente en la superficie de los conductores, dejando libre de carga el interior.
  Un conductor que se encuentra en equilibrio eléctrico tiene su exceso de carga repartido por su superficie. El potencial eléctrico en cualquier punto de su interior y de su superficie es el mismo y elcampo eléctrico en su interior es nulo.
  Cada campo eléctrico puede ser definido en cada uno de sus puntos por dos magnitudes: la intensidad del campo eléctrico y el potencial eléctrico. ¿Qué ocurre cuando introducimos una carga q en el interior de uno de ellos?¿Hacia donde se mueve?. A lo largo de este apartado vamos a estudiar que ocurre con dicha carga desde el punto de vista de la fuerza eléctrica y del potencial eléctrico.

  Movimiento en base a la Fuerza Eléctrica

  Si partimos de la definición de intensidad de campo eléctrico, sabemos que la fuerza eléctrica que sufre una carga q en un punto es:

  E⃗ =F⃗ q⇒F⃗ =q⋅E⃗ 

  
  

  De aquí podemos deducir que:

  • Si la carga es positiva ( q > 0 ), la fuerza eléctrica tendrá el mismo signo que el campo y por tanto q se moverá en el sentido del campo.
  • Si la carga es negativa ( q < 0 ), la fuerza eléctrica tendrá distinto signo que el campo y por tanto q se moverá en sentido contrario al campo.

  Las cargas positivas se mueven en el sentido del campo eléctrico y las cargas negativas se mueven en sentido contrario.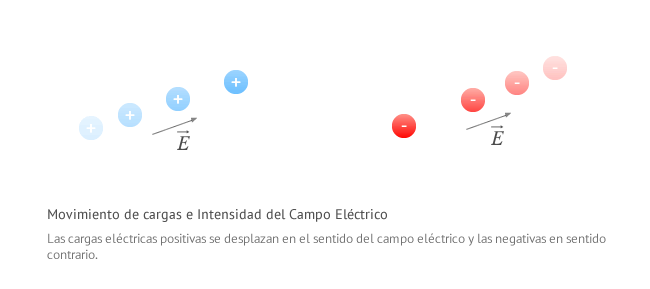

  

  Movimiento en base al Potencial Eléctrico

  Cuando estudiamos el potencial eléctrico, definimos la diferencia de potencial entre dos puntos de la siguiente forma

  VB−VA=−We(A→B)q

  
  

  Tal y como vimos en el apartado del trabajo eléctrico, el trabajo realizado por una fuerza eléctrica para desplazar una carga q desde un punto A a otro B, sin presencia de fuerzas externas, es un valor positivo. Si analizamos que ocurre si la carga q es positiva o negativa, obtenemos que:

  q < 0	VB-VA >0 => VB>VA	La carga se mueve desde puntos de menor potencial a mayor potencial
  q > 0	VB-VA<0 => VB<VA	Se mueve desde puntos de mayor potencial a menor potencial

  Por tanto:

  • Las cargas positivas se mueven desde zonas de mayor potencial eléctrico a zonas de menor potencial eléctrico.
  • Las cargas negativas se mueven desde zonas de menor potencial eléctrico a zonas de mayor potencial eléctrico.

  Teniendo en cuenta que tal y como hemos estudiado anteriormente, las cargas positivas se mueven en el sentido de la intesidad de campo eléctrico entonces, dicha intensidad se dirige siempre desde zonas de mayor potencial a zonas de menor potencial.

  La intensidad de campo eléctrico apunta siempre hacia potenciales decrecientes.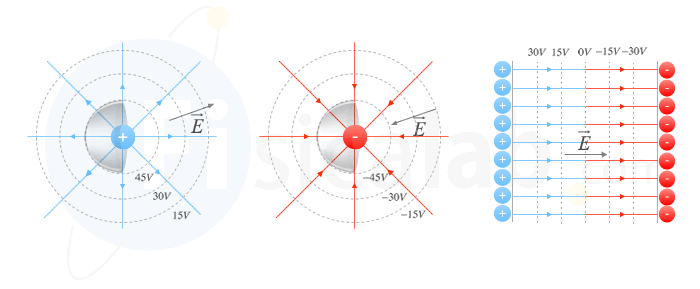

  
  A partir de esta realidad, podemos definir una nueva magnitud escalar denominada capacidad eléctrica.no depende de la carga testigo q' que introducimos para medirlo.

Trabajo Eléctrico

Si aplicas una fuerza sobre un objeto y este se desplaza decimos que la fuerza que estás ejerciendo realiza un trabajo. Del mismo modo, si un cuerpo se desplaza bajo la acción de una fuerza eléctrica, dicha fuerza realiza también un trabajo denominado trabajo eléctrico.

El trabajo eléctrico realizado para desplazar una carga desde un punto A hasta otro B se obtiene por medio de la siguiente expresión

We(A→B)=∫BAF⃗ e⋅dl⃗ 

donde:

• We(A→B) es el trabajo eléctrico. En el S.I. se mide en Julios (J).
• F⃗ e es la Fuerza eléctrica que sufre la carga. En el S.I. se mide en Newtons (N).
• dl⃗  es un vector infinitesimal tangente a cada punto de la trayectoria seguida por la carga mientras se desplaza entre A y B. En el S.I. se mide en metros (m).

La fuerza eléctrica descrita por la ley de Coulomb, al igual que otras fuerzas como la fuerza elástica o la fuerza gravitatoria, es una fuerza central y por tanto es una fuerza conservativa. Esto implica que:

• El trabajo que realiza una fuerza eléctrica para mover un cuerpo cargado desde una posición A hasta otra B, únicamente depende de dichas posiciones y no del camino seguido para llegar de A a B.
• Cuando el camino que sigue el cuerpo entre A y B es un camino cerrado o un ciclo, el trabajo eléctrico es nulo.

Trabajo realizado por un campo eléctrico formado por una carga puntual

Cuando una carga Q crea un campo eléctrico en el que se introduce otra carga q, esta última sufrirá una fuerza eléctrica. El trabajo que realiza dicha fuerza para trasladar q desde un punto A a otro B cualesquiera es:

We(A→B) =∫BAF⃗ edl⃗ =−(K⋅Q⋅qrB−K⋅Q⋅qrA)

O de forma más simplificada:

We(A→B)=−K⋅Q⋅q⋅[1rB−1rA]

donde:

• K es una constante de proporcionalidad llamada constante de la ley de Coulomb. No se trata de una constante universal y depende del medio en el que se encuentren las cargas. En concreto para el vacío k es aproximadamente 9·109 N·m2/C2 utilizando unidades en el S.I.
• Q y q son lo valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
• rA es el valor de la distancia que separa Q y el punto A y rB es el valor de la distancia que separa Q y el punto B. En el S.I. se miden en metros (m).

Demostración

Para demostrar la expresión anterior, tendremos en cuenta la definición de trabajo eléctrico y la definición deproducto escalar:

F⃗ e⋅dl⃗  = Fe⋅dl⋅cos α

Si observas la siguiente figura genérica que representa el desplazamiento de una carga entre dos puntos, puedes comprobar que dr = dl · cos α:

Fe⋅dl⋅cos α = Fe⋅dr

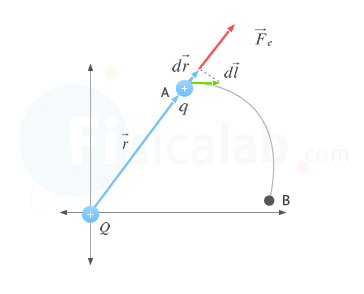
Desarrollando la integral, obtenemos que:

We(A→B)=∫BAF⃗ e⋅dl⃗  ⇒We(A→B)=∫BAFe⋅dl ⋅ cos α ⇒We(A→B)=∫BAFe⋅dr ⇒We(A→B)=K⋅Q⋅q⋅∫BA1r2⋅dr ⇒We(A→B)=K⋅Q⋅q⋅[−1r]BA⇒We(A→B)=−K⋅Q⋅q⋅[1rB−1rA]

¿Cómo interpretar el signo en el Trabajo Eléctrico?

Es lógico pensar que si sobre una carga actúa una fuerza eléctrica, esta carga se deberá desplazar en el sentido y dirección de dicha fuerza, al igual que si aplicas una fuerza sobre una taza situada sobre una mesa esta se desplazará en su misma dirección y sentido. ¿no?. Sin embargo, en muchas ocasiones te encontrarás con que la carga que estudias no se desplaza en dicha dirección. Esto implica que con toda probabilidad debe existir otra fuerza externa que altera el desplazamiento natural.

¿Cómo afecta esto al trabajo eléctrico?. Cuando calculamos el valor del trabajo eléctrico realizado por una fuerza eléctrica este será positivo si la fuerza favorece al desplazamiento natural de q y negativa si se opone a dicho desplazamiento natural. Por tanto, si el trabajo eléctrico es negativo debe existir obligatoriamente una fuerza externa que realiza un trabajo externo (Wf) que debe contrarrestar al menos el trabajo eléctrico. De tal forma que:

We=−Wf

donde:

• We es el trabajo realizado por la fuerza eléctrica para moverlo desde A hasta B.
• Wf es el trabajo realizado por la fuerza externa para moverlo desde A hasta B.

Al igual que cuando hablamos de la energía potencial gravitatoria estudiamos que un cuerpo que se encuentra a una determinada altura de la superficie de la Tierra adquiere una determinada cantidad de energía potencial provocada por la acción de la fuerza gravitatoria, un cuerpo cargado que sufre la acción de una fuerza eléctrica adquiere energía potencial eléctrica (Ep).

El trabajo realizado por la fuerza eléctrica para trasladar una carga desde un punto A a otro B se puede expresar de la siguiente forma:

We(A→B) =∫BAF⃗ edl⃗ =−∆Ep=−(EpB−EpA)

Esta expresión determina que sólo es posible calcular diferencias de energía (ΔEp) y la energía potencial en un punto es siempre un valor relativo con respecto a otro, sin embargo para hablar de un valor absoluto se utiliza como referencia un punto situado en el infinito. Dado que a esa distancia no existe fuerza eléctrica que atraiga o repela las cargas, la energía potencial eléctrica allí es nula. Por tanto, aplicando esta consideración obtenemos que:

We(∞→A) =∫A∞F⃗ edl⃗ =−∆Ep=−(EpA−Ep∞)=−EpA

Tal y como estudiamos en el apartado de trabajo eléctrico, si sobre una carga actúa otra fuerza externa (a parte de la fuerza eléctrica), se cumple que:

We=−Wf

donde:

• We es el trabajo realizado por la fuerza eléctrica para moverlo desde A hasta B.
• Wf es el trabajo realizado por la fuerza externa para moverlo desde A hasta B.

Por esta razón, podemos definir el trabajo realizado por la fuerza externa para trasladar la carga desde el infinito hasta una posición A como:

Wf(∞→A) =−We(∞→A) = EpA

La energía potencial eléctrica de una carga situada en una posición A equivale al trabajo realizado por una fuerza externa para trasladar dicha carga desde el infinito hasta dicha posición A, o dicho de otra forma, el opuesto del trabajo realizado por la fuerza eléctrica para llevarla desde el infinito hasta A.

EpA=Wf(∞→A) =−We(∞→A) 

Energía potencial de un sistema de dos partículas

Si disponemos de dos cargas Q y q, el trabajo para aproximar q desde el infinito hasta un punto A próximo a Q se puede obtener aplicando la definición de trabajo entre dos puntos:

We(∞→A)=∫A∞F⃗ edl⃗ =∫A∞Fedr =−K⋅Q⋅q⋅∫A∞1r2dr ⇒We(∞→A)=−K⋅Q⋅q⋅[−1r]A∞⇒We(∞→A)=−K⋅Q⋅qr

Sustituyendo por la definición de energía potencial:

EpA=K⋅Q⋅qr

La energía potencial eléctrica que posee una carga puntual q en presencia de otra carga puntual Q que se encuentran separadas cierta distancia r es:

Ep=K⋅Q⋅qr

donde:

• Ep es la energía potencial eléctrica. En el S.I. se mide en Julios (J).
• Q y q son los valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
• r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
• K es la constante de la ley de Coulomb. Para el vacío su valor es aproximadamente 9·109 N·m2/C2utilizando unidades en el S.I.

Como ya hablamos en el apartado de trabajo eléctrico, este es el trabajo que realizan las fuerzas eléctricas y no debemos confundirlo con el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). El trabajo que realiza dicha fuerza (Wf) se relaciona con el trabajo eléctrico (We) y la energía potencial eléctrica de la siguiente forma :

We=−Wf=−ΔEp

A continuación, vamos a estudiar que esta relación se cumple en los dos casos comentados anteriormente.

Cargas con distinto signo

Imagina dos cargas fijas, una positiva y otra negativa. En principio, dado que se tratan de cargas con distinto signo en cada una de ellas aparecerá una fuerza de atracción hacia la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más alejado. Al hacer esto:

• Si aplicas la definición de trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
• Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
• Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).

En resumidas cuentas, el trabajo que realiza la fuerza externa al alejarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de acercarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.

Cargas del mismo signo

Ahora, imagina dos cargas fijas del mismo signo (positiva o negativa). En principio, dado que se tratan de cargas con signos iguales en cada una de ellas aparecerá una fuerza de repulsión en contra de la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más cercano. Al hacer esto, como en el caso anterior:

• Si aplicas la definición de trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
• Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
• Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).

El trabajo que realiza la fuerza externa al acercarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de alejarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.

Fíjate que tal y como indicamos en la fórmula inicial, cuando se aplica la fuerza externa, el signo del trabajo del campo eléctrico es exactamente el contrario al del trabajo realizado por la fuerza eléctrica y al de la diferencia de energía potencial.

Energía potencial eléctrica de un sistema de más de dos partículas

Si en lugar de poseer dos cargas puntuales, disponemos de más cargas, podemos calcular la energía potencial del sistema sumando algebraicamente  la energía potencial eléctrica entre cada pareja de cargas. Por ejemplo, si disponemos de tres cargas q1, q2 y q3 la energía potencial eléctrica del sistema se obtiene por medio de la siguiente expresión:

Ep=K⋅q1⋅q2r1,2+K⋅q1⋅q3r1,3+K⋅q2⋅q3r2,3

La energía potencial de un sistema formado por varias cargas puntuales equivale al trabajo necesario que debería realizar una fuerza exterior para ensamblar las cargas en esas posiciones trayéndolas desde el infinito.

Energía potencial eléctrica y energía cinética

Si dos o más cargas puntuales se enceuentran sometidas únicamente a la fuerza eléctrica, la energía total del sistema es siempre la misma (permanece constante). Esto es debido a que la fuerza eléctrica es una fuerza conservativa. ¿Que consideraciones tiene esto?. En primer lugar, que la suma de la energía cinética y la energía potencial de el sistema es independiente del punto en que se encuentre, por tanto entre dos puntos A y B se cumple que:

EcA+EpA=EcB+EpB

De igual forma, si disminuye la energía cinética, aumentará la energía potencial y viceversa. De esta forma también se cumple que:

Campo eléctrico

Al introducir una carga en el espacio esta crea en su entorno un área de influencia de tal forma que si introducimos otra carga testigo en dicha área sufrirá la acción de una fuerza eléctrica debido a la ley de Coulomb.

Campo eléctrico es la perturbación que genera una carga eléctrica en el espacio que le rodea.

Diferencia entre acción a distancia y campo

En ocasiones se suelen confundir los conceptos de acción a distancia y campo, sin embargo existen diferencias sustanciales que deben tenerse en cuenta:

• Acción a distancia. En una acción a distancia una partícula actúa directamente e instantáneamente sobre otra partícula sin que le medio que les rodea intervenga.
• Campo. En un campo, la partícula perturba las propiedades del espacio que le rodea. Los valores de dichas propiedades dependen de la posición y definen el campo. Esto hace que sea directamente el campo el que interactúe con una partícula lejana que se introduzca en el espacio del campo. Por tanto, la interacción que se produce no es intantánea como ocurre en la acción a distancia y la velocidad de propagación es finita.

Propiedades que definen el campo eléctrico

Los campos eléctricos vienen determinados en cada posición por el valor de la intensidad de campo eléctricoy el potencial eléctrico. En concreto, la intensidad de campo eléctrico en cada punto ofrece una visión dinámica de la interacción electrostática y el potencial eléctrico un visión desde un punto de vista energético.

Esto es debido a que al introducir en un campo eléctrico una carga testigo, esta dependiendo de su posición:

• Sufrirá la acción de una fuerza eléctrica. (visión dinámica)
• Adquirirá una energía potencial. (visión energética)