La energía mecánica de un cuerpo es la capacidad que tiene de realizar un trabajo mecánico, es decir, de producir un movimiento. En este apartado vamos a estudiar:
- El concepto de energía mecánica
- El principio de conservación de la energía
- El principio de conservación de la energía cuando hay fuerzas no conservativas, como la de rozamiento
- Qué ocurre con la energía mecánica en los choques
Energía Mecánica
La rama de la física que estudia y analiza el movimiento y reposo de los cuerpos, y su evolución en el tiempo, bajo la acción de fuerzas se denomina mecánica. En un cuerpo existen fundamentalmente dos tipos de energía que pueden influir en su estado de reposo o movimiento: la energía cinética y la potencial.
Llamamos energía mecánica de un cuerpo a la suma de la energía cinética Ec y potencial Ep que posee:
Es importante señalar que la energía potencial, de modo general, cuenta con distintas contribuciones. En este tema nos centraremos en la energía potencial gravitatoria y la energía potencial elástica.
Principio de Conservación de la Energía Mecánica
La energía mecánica de un cuerpo se mantiene constante cuando todas las fuerzas que actúan sobre él son conservativas.
Es probable que en numerosas ocasiones hayas oido decir que "la energía ni se crea ni se destruye, solo se transforma". En realidad, tal afirmación es uno de los principios más importantes de la Física y se denomina Principio de Conservación de la Energía. Vamos a particularizarlo para el caso de la energía mecánica.
Para ententer mejor este concepto vamos a ilustrarlo con un ejemplo. Imagina una pelota colgada del techo que cae sobre un muelle. Según el principio de conservación de la energía mecánica, la energía mecánica de la bola es siempre la misma y por tanto durante todo el proceso dicha energía permanecerá constante, tan solo cambiarán las aportaciones de los distintos tipos de energía que conforman la energía mecánica.
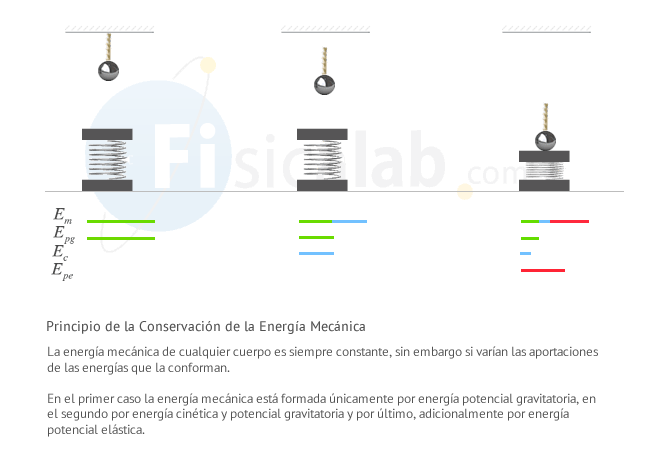
Antes de caer, la energía mecánica de la bola está formada únicamente por energía potencial gravitatoria. Al caer y adquirir una velocidad, la energía potencial gravitatoria se convierte en energía cinética, dejando constante la energía mecánica. Por último, al impactar contra el muelle, lo comienza a comprimir, provocando que la energía mecánica se componga de energía cinética, energía potencial gravitatoria y energia potencial elástica.
Comprobación del Principio de Conservación de la Energía Mecánica
Para comprobar el principio de conservación de la energía mecánica razonamos de la siguiente manera:
- El teorema de la energía cinética establece que la variación de energía cinética ∆Ec entre dos puntos (la cual se traduce en una variación de su velocidad) que sufre un cuerpo es igual al trabajo realizado por la fuerza resultante que actua sobre el cuerpo entre los puntos inicial y final. Esto se cumple tanto si las fuerzas son conservativas como si no.
- Por otro lado, en el caso de fuerzas conservativas, dicho trabajo coincide con la variación de energía potencial cambiada de signo.
- De lo anterior, y teniendo en cuenta que en ambos casos nos referimos al mismo trabajo, podemos escribir:
- Por tanto la energía mecánica no cambia, permanece constante
Principio de Conservación de la Energía con Fuerzas no Conservativas
En el caso general de que en nuestro sistema aparezcan fuerzas no conservativas, la energía mecánica no se conserva. Existen dos contribuciones para el trabajo total Wt:
- Trabajo de fuerzas conservativas Wc
- Trabajo de fuerzas no conservativas Wnc
Por tanto:
Si sobre un cuerpo actúan fuerzas conservativas y no conservativas, la variación de energía mecánica coincide con el trabajo realizado por las fuerzas no conservativas
La fuerza de rozamiento es uno de los casos más destacados de fuerza no conservativa o disipativa. Imagina el caso sencillo en que lanzas una canica deslizándose por el suelo a cierta velocidad. Al cabo de un tiempo, esta acabará por pararse. La energía mecánica de la canica está formada únicamente por su energía cinética (Em=Ec+Ep ). Suponiendo la fricción con el aire despreciable, la fuerza de rozamiento, disipativa, va a ser la responsable de que nuestra canica vaya, poco a poco, perdiendo su energía mecánica (coincidente en este caso con la cinética).
La energía mecánica de un cuerpo es la capacidad que tiene de realizar un trabajo mecánico, es decir, de producir un movimiento. En este apartado vamos a estudiar:
- El concepto de energía mecánica
- El principio de conservación de la energía
- El principio de conservación de la energía cuando hay fuerzas no conservativas, como la de rozamiento
- Qué ocurre con la energía mecánica en los choques
¿Empezamos?
Energía Mecánica
La rama de la física que estudia y analiza el movimiento y reposo de los cuerpos, y su evolución en el tiempo, bajo la acción de fuerzas se denomina mecánica. En un cuerpo existen fundamentalmente dos tipos de energía que pueden influir en su estado de reposo o movimiento: la energía cinética y la potencial.
Llamamos energía mecánica de un cuerpo a la suma de la energía cinética Ec y potencial Ep que posee:
Es importante señalar que la energía potencial, de modo general, cuenta con distintas contribuciones. En este tema nos centraremos en la energía potencial gravitatoria y la energía potencial elástica.
Principio de Conservación de la Energía Mecánica
La energía mecánica de un cuerpo se mantiene constante cuando todas las fuerzas que actúan sobre él son conservativas.
Es probable que en numerosas ocasiones hayas oido decir que "la energía ni se crea ni se destruye, solo se transforma". En realidad, tal afirmación es uno de los principios más importantes de la Física y se denomina Principio de Conservación de la Energía. Vamos a particularizarlo para el caso de la energía mecánica.
Para ententer mejor este concepto vamos a ilustrarlo con un ejemplo. Imagina una pelota colgada del techo que cae sobre un muelle. Según el principio de conservación de la energía mecánica, la energía mecánica de la bola es siempre la misma y por tanto durante todo el proceso dicha energía permanecerá constante, tan solo cambiarán las aportaciones de los distintos tipos de energía que conforman la energía mecánica.

Antes de caer, la energía mecánica de la bola está formada únicamente por energía potencial gravitatoria. Al caer y adquirir una velocidad, la energía potencial gravitatoria se convierte en energía cinética, dejando constante la energía mecánica. Por último, al impactar contra el muelle, lo comienza a comprimir, provocando que la energía mecánica se componga de energía cinética, energía potencial gravitatoria y energia potencial elástica.
Comprobación del Principio de Conservación de la Energía Mecánica
Para comprobar el principio de conservación de la energía mecánica razonamos de la siguiente manera:
- El teorema de la energía cinética establece que la variación de energía cinética ∆Ec entre dos puntos (la cual se traduce en una variación de su velocidad) que sufre un cuerpo es igual al trabajo realizado por la fuerza resultante que actua sobre el cuerpo entre los puntos inicial y final. Esto se cumple tanto si las fuerzas son conservativas como si no.
- Por otro lado, en el caso de fuerzas conservativas, dicho trabajo coincide con la variación de energía potencial cambiada de signo.
- De lo anterior, y teniendo en cuenta que en ambos casos nos referimos al mismo trabajo, podemos escribir:
- Por tanto la energía mecánica no cambia, permanece constante
Principio de Conservación de la Energía con Fuerzas no Conservativas
En el caso general de que en nuestro sistema aparezcan fuerzas no conservativas, la energía mecánica no se conserva. Existen dos contribuciones para el trabajo total Wt:
- Trabajo de fuerzas conservativas Wc
- Trabajo de fuerzas no conservativas Wnc
Por tanto:
Si sobre un cuerpo actúan fuerzas conservativas y no conservativas, la variación de energía mecánica coincide con el trabajo realizado por las fuerzas no conservativas
La fuerza de rozamiento es uno de los casos más destacados de fuerza no conservativa o disipativa. Imagina el caso sencillo en que lanzas una canica deslizándose por el suelo a cierta velocidad. Al cabo de un tiempo, esta acabará por pararse. La energía mecánica de la canica está formada únicamente por su energía cinética (Em=Ec+Ep ). Suponiendo la fricción con el aire despreciable, la fuerza de rozamiento, disipativa, va a ser la responsable de que nuestra canica vaya, poco a poco, perdiendo su energía mecánica (coincidente en este caso con la cinética).
Comprobación del Principio de Conservación de la Energía en Presencia de Fuerzas No Conservativas
Para comprobar el Principio de conservación de la energía mecánica razonamos de la siguiente manera:
Wt=Wnc+Wc - Por el Teorema de la Energía Cinética,
Wt=ΔEc - Por otro lado, las fuerzas conservativas cumplen que
Wc=−ΔEp Wt=Wnc+Wc⇒ΔEc=Wnc−ΔEp⇒Δ⎛⎝⎜⎜Ec+EpEm⎞⎠⎟⎟=Wnc⇒ΔEm=Wnc
Choques Elásticos e Inelásticos
El estudio de los choques en Física tiene un gran interés para distintos campos, como por ejemplo, el de la seguridad automovilística o el de la seguridad en las carreras de competición de fórmula 1.
Según el principio de conservación del momento lineal , el momento lineal p→ del sistema se mantiene constante antes y después del choque. Podemos distinguir dos tipos de choques:
- Elásticos: Los cuerpos no sufren deformaciones. Todas las fuerzas son conservativas y por tanto se mantiene, además, la energía mecánica del conjunto.Suponiendo un choque entre dos bolas de masa m1 y m2 que viajan antes del choque a
v→1 yv→2 respectivamente, y después del choque av→´1 yv→´2 respectivamente, nos queda que se deben cumplir de forma simultánea las siguientes expresiones: - Inelásticos: Los cuerpos sufren deformaciones. El principio de conservación del momento lineal se mantiene vigente. Sin embargo intervienen fuerzas no conservativas que hacen que la energía mecánica se disipe. Por tanto la energía cinética del sistema se disipa. Es el caso, por ejemplo, de las vallas elásticas de seguridad de algunos circuitos de competición.
Lanzamos una bola de 2 kg de peso en linea recta a una velocidad de 4 m/s rodando por el suelo. Sabiendo que recorre 20 m antes de detenerse y suponiendo que la fricción con el aire es nula, calcula el valor de la fuerza de rozamiento con el suelo.
Solución
Datos
- Masa del cuerpo: m = 2 kg
- Velocidad del cuerpo (módulo): v = 4 m/s
- Desplazamiento (módulo): ∆r = 20 m
Consideraciones previas
- Para el estudio que nos ocupa, podemos considerar que la energía potencial es nula y por tanto el incremento de la energía mecánica coincide con el incremento de la energía cinética
- Dado que el cuerpo acaba deteniéndose, la energía cinética final es cero (
Ecf=0 ) - El ángulo que forma la fuerza de rozamiento con el vector desplazamiento es de 180 grados (π rad)
Resolución
Con las consideraciones anteriores nos queda:
No hay comentarios.:
Publicar un comentario